Up
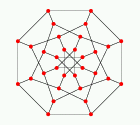
Dyck graph
There is a unique cubic symmetric (i.e., both vertex- and
edge-transitive) graph on 32 vertices known as the Dyck graph.
Construction
The Dyck graph is the graph that has as vertices the triangles
in the Shrikhande graph,
adjacent when they share an edge.
Group
The group is (4x4):3:2:2 of order 192.
It is vertex- and edge-transitive, with vertex stabilizer Sym(3).
Spectrum
The Dyck graph has spectrum
±31, (±√5)6, ±19,
and is the unique graph with this spectrum.
Distribution diagram
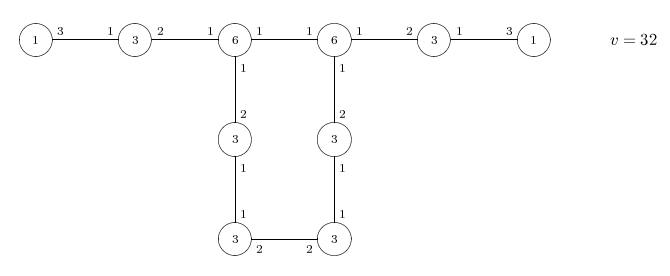
Every vertex has a unique special antipode at distance 5,
but interchanging special antipodes is not a graph automorphism.
The graph is bipartite. The two components of the distance-2 graph
are copies of the Shrikhande graph.
The diameter is 5, the girth 6.
References
Walther Dyck,
Über Aufstellung und Untersuchung von Gruppe und Irrationalität
regulärer Riemann'scher Flächen,
Math. Ann. 17 (1880) 473-509.
Wolfram, Dyck Graph.
Cubic symmetric xyz graphs.


