Up

Coxeter graph

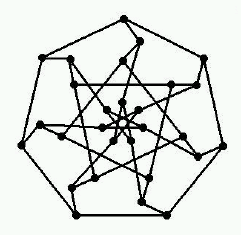
There is a unique distance-regular graph with intersection array {3,2,2,1;1,1,1,2}. It has 28 vertices and spectrum 31 28 (√2 – 1)6 (–1)7 (–√2 – 1)6. This is the graph that Coxeter calls "My graph".

Group

The full group of automorphisms is PGL(2,7) = L3(2).2, acting distance-transitively with point stabilizer D12. It is 3-arc-transitive.

Construction

This is the graph on the triangles in the Fano plane, where triangles are adjacent when they are disjoint.

Equivalently, this is the graph on the antiflags of the Fano plane, where (P,L) is adjacent to (Q,M) when P,Q are not on L,M.

Supergraphs

The Coxeter graph is a subgraph of the Odd graph O4 (of the disjoint triples of a 7-set), and hence also of the Hoffman-Singleton graph.

Subgraphs

Substructures belonging to the maximal subgroups of the automorphism group:

a) partition into three 7-gons and a 7-coclique There are 8 of these, forming a single orbit. The stabilizer of one is 7:6, with vertex orbit sizes 7+21. (There are 24 heptagons. The set of 7 neighbours of a heptagon is a 7-coclique corresponding to a Fano plane. There are 8 such Fano 7-cocliques, each adjacent to three heptagons.)

b) A 4-set, all mutual distances 4. There are 14 of these, forming a single orbit. The stabilizer of one is S4, with vertex orbit sizes 4+12+12. These correspond to the antiflags containing a given point or a given line. The graph on these 4-sets, adjacent when they have nonempty intersection, is the Heawood graph.

c) A pair of edges at distance 4. There are 21 of these, forming a single orbit. The stabilizer of one is D16, with vertex orbit sizes 4+8+8+8. These correspond to the flags of the Fano plane.

d) A vertex. There are 28 of these, forming a single orbit. The stabilizer of one is D12, with vertex orbit sizes 1+3+6+12+6. These correspond to the antiflags of the Fano plane.

Circuits and Hamiltonicity

The Coxeter graph is maximally non-Hamiltonian: there is a Hamiltonian path between any two nonadjacent vertices.

The girth is 7. The binary code generated by the cycles has parameters [42,15,7], with weight enumerator 

 0:  1
 7:  24
 8:  21
 9:  56
10:  84
12:  140
13:  336
14:  528
15:  896
16:  987
17:  1344
18:  2296
19:  3024
20:  3360
21:  3760
22:  4368
23:  4200
24:  3087
25:  2184
26:  1428
27:  560
28:  84
Thus, there are 24 7-gons and 21 8-gons and no 11-gons. The 84 words of weight 28 are disjoint unions of two 14-gons - their complements are the 84 complete matchings. In particular, the Coxeter graph is 3-edge-colorable. (By Brooks' theorem it is also 3-colorable.)

References

H.S.M. Coxeter, My graph, Proc. London Math. Soc. 46 (1983) 117-136.

[BCN], Section 12.3.