Optimizacijske metode

« nazaj

Optimizacijske metode - vaje 21.5.2021

Problem vezanega ekstrema z neenačbami

Naloga 1

Poišči minimum in maksimum funkcije $f(x, y, z) = x+y+z$ v $\mathbb{R}^3$ pri pogoju $x^2+y^2 \le z \le 1$.

\[\begin{aligned} f_{\min} &= x+y+z & \text{linearna} \\ f_{\max} &= -x-y-z & \text{linearna} \\ g_1 &= x^2 + y^2 - z & \text{konveksna} \\ g_2 &= z - 1 & \text{linearna} \\ H_{g_1} &= \begin{pmatrix} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 0 \end{pmatrix} \ge 0 \end{aligned}\]

Minimum

\[\begin{aligned} L &= x + y + z + \lambda_1 (x^2 + y^2 - z) + \lambda_2 (z - 1) \\ L_x &= 1 + 2 \lambda_1 x = 0 \\ L_y &= 1 + 2 \lambda_1 y = 0 \\ L_z &= 1 - \lambda_1 + \lambda_2 = 0 \\ \lambda_1 &> 0 \\ g_1 &= 0 \\ x &= y < 0 \\ z &= 2x^2 \end{aligned}\]
  1. \[\begin{aligned} g_2 &= 0 \\ z &= 1 = 2x^2 \\ x &= y = -\sqrt{2}/2 \\ L_x &= 1 - \lambda_1 \sqrt{2} = 0 \\ L_y &= 1 - \lambda_1 \sqrt{2} = 0 \\ L_z &= 1 - \lambda_1 + \lambda_2 = 0 \\ \lambda_1 &= \sqrt{2}/2 \ge 0 \\ \lambda_2 &= \sqrt{2}/2 - 1 < 0 \end{aligned}\]
  2. \[\begin{aligned} \lambda_2 &= 0 \\ L_x &= 1 + 2 \lambda_1 x = 0 \\ L_y &= 1 + 2 \lambda_1 y = 0 \\ L_z &= 1 - \lambda_1 = 0 \\ \lambda_1 &= 1 \\ x &= y = -1/2 \\ z &= 1/2 \\ g_2 &= 1/2 - 1 = -1/2 \le 0 \end{aligned}\]

Minimum: $(x, y, z) = (-1/2, -1/2, 1/2)$

Maksimum

\[\begin{aligned} L &= -x - y - z + \lambda_1 (x^2 + y^2 - z) + \lambda_2 (z - 1) \\ L_x &= -1 + 2 \lambda_1 x = 0 \\ L_y &= -1 + 2 \lambda_1 y = 0 \\ L_z &= -1 - \lambda_1 + \lambda_2 = 0 \\ \lambda_1 &> 0 \\ g_1 &= 0 \\ x &= y > 0 \\ z &= 2x^2 \end{aligned}\]
  1. \[\begin{aligned} g_2 &= 0 \\ z &= 1 = 2x^2 \\ x &= y = \sqrt{2}/2 \\ L_x &= -1 + \lambda_1 \sqrt{2} = 0 \\ L_y &= -1 + \lambda_1 \sqrt{2} = 0 \\ L_z &= -1 - \lambda_1 + \lambda_2 = 0 \\ \lambda_1 &= \sqrt{2}/2 \ge 0 \\ \lambda_2 &= 1 + \sqrt{2}/2 \ge 0 \end{aligned}\]

Maksimum: $(x, y, z) = (\sqrt{2}/2, \sqrt{2}/2, 1)$

Naloga 2

Poišči optimalno rešitev problema vezanih ekstremov z neenačbami

\[\begin{aligned} \min &\quad x^2 + y^2 + z^2 + 2xz - 3x - z + 2 \\[1ex] &\quad x - y \le 1 \\ &\quad y - z \le 3 \ . \end{aligned}\]
\[\begin{aligned} f &= x^2 + y^2 + z^2 + 2xz - 3x - z + 2 & \text{konveksna} \\ g_1 &= x - y - 1 & \text{linearna} \\ g_2 &= y - z - 3 & \text{linearna} \\ H_f &= \begin{pmatrix} 2 & 0 & 2 \\ 0 & 2 & 0 \\ 2 & 0 & 2 \end{pmatrix} \ge 0 \\[1ex] L_x &= 2x + 2z - 3 + \lambda_1 = 0 \\ L_y &= 2y - \lambda_1 + \lambda_2 = 0 \\ L_z &= 2x + 2z - 1 - \lambda_2 = 0 \\ \lambda_1 &\ne \lambda_2 \end{aligned}\]

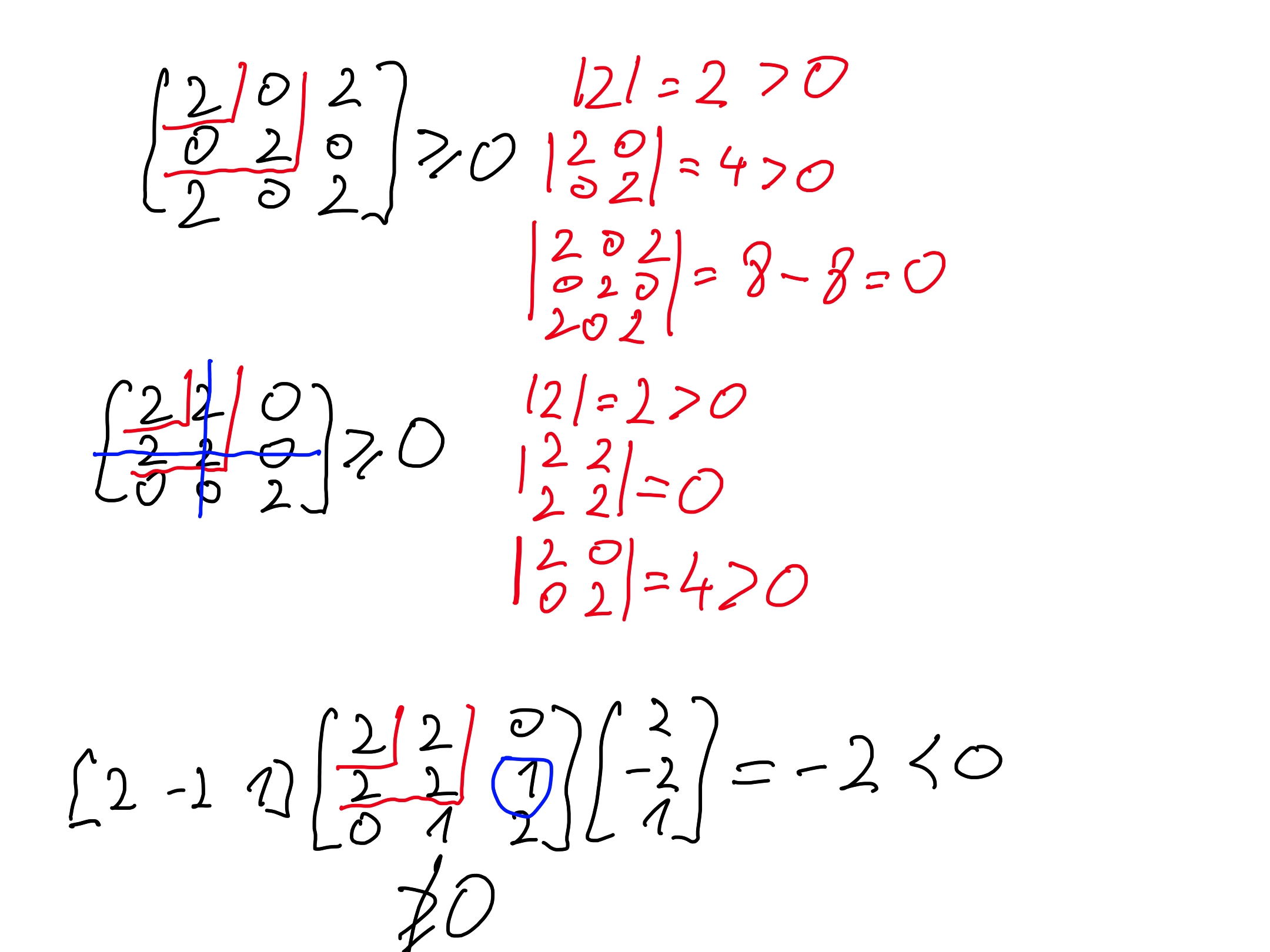
  1. \[\begin{aligned} g_1 &= 0 \\ y &= x - 1 \\ g_2 &= x - z - 4 \\ L_x &= 2x + 2z - 3 + \lambda_1 = 0 \\ L_y &= 2x - 2 - \lambda_1 + \lambda_2 = 0 \\ L_z &= 2x + 2z - 1 - \lambda_2 = 0 \\ \end{aligned}\]
    1. \[\begin{aligned} g_2 &= 0 \\ z &= x - 4 \\ L_x &= 4x - 11 + \lambda_1 = 0 \\ L_y &= 2x - 2 - \lambda_1 + \lambda_2 = 0 \\ L_z &= 4x - 9 - \lambda_2 = 0 \\ L_x + L_y + L_z &= 10x - 22 = 0 \\ x &= 11/5 \\ \lambda_1 &= 11 - 44/5 = 11/5 \ge 0 \\ \lambda_2 &= 44/5 - 9 = -1/5 < 0 \end{aligned}\]
    2. \[\begin{aligned} g_2 &< 0 \\ \lambda_2 &= 0 \\ L_x &= 2x + 2z - 3 + \lambda_1 = 0 \\ L_y &= 2x - 2 - \lambda_1 = 0 \\ L_z &= 2x + 2z - 1 = 0 \\ L_x - L_z &= -2 + \lambda_1 = 0 \\ \lambda_1 &= 2 \ge 0 \\ x &= 2 \\ z &= -3/2 \\ y &= 1 \\ g_2 &= 1 + 3/2 - 3 = -1/2 < 0 \end{aligned}\]

Optimalna rešitev: $(x, y, z) = (2, 1, -3/2)$

Naloga 3

Poišči optimalno rešitev problema vezanih ekstremov z neenačbami

\[\begin{aligned} \min &\quad 3x^2 + 2xy + 3y^2 - 12x - 4y \\[1ex] 2x + y &\le 1 \\ x &\ge 0 \\ x+y &\ge 0 \ . \end{aligned}\]
\[\begin{aligned} f &= 3x^2 + 2xy + 3y^2 - 12x - 4y & \text{konveksna} \\ g_1 &= 2x + y - 1 & \text{linearna} \\ g_2 &= -x & \text{linearna} \\ g_3 &= -x - y & \text{linearna} \\ H_f &= \begin{pmatrix} 6 & 2 \\ 2 & 6 \end{pmatrix} \ge 0 \\ \det H_f &= 6 \cdot 6 - 2 \cdot 2 = 32 \ge 0 \\[1ex] L_x &= 6x + 2y - 12 + 2 \lambda_1 - \lambda_2 - \lambda_3 = 0 \\ L_y &= 2x + 6y - 4 + \lambda_1 - \lambda_3 = 0 \end{aligned}\]
  1. \[\begin{aligned} g_2 &= 0 \\ x &= 0 \\ g_1 &= y - 1 \\ g_3 &= -y \\ L_x &= 2y - 12 + 2 \lambda_1 - \lambda_2 - \lambda_3 = 0 \\ L_y &= 6y - 4 + \lambda_1 - \lambda_3 = 0 \end{aligned}\]
    1. \[\begin{aligned} g_3 &= 0 \\ y &= 0 \\ g_1 &= -1 < 0 \\ \lambda_1 &= 0 \\ L_x &= -12 - \lambda_2 - \lambda_3 = 0 \\ L_y &= -4 - \lambda_3 = 0 \\ \lambda_3 &= -4 < 0 \end{aligned}\]
    2. \[\begin{aligned} g_3 &< 0 \\ \lambda_3 &= 0 \\ L_x &= 2y - 12 + 2 \lambda_1 - \lambda_2 = 0 \\ L_y &= 6y - 4 + \lambda_1 = 0 \end{aligned}\]
      1. \[\begin{aligned} g_1 &= 0 \\ y &= 1 \\ g_3 &= -1 < 0 \\ L_x &= -10 + 2 \lambda_1 - \lambda_2 = 0 \\ L_y &= 2 + \lambda_1 = 0 \\ \lambda_1 &= -2 < 0 \end{aligned}\]
      2. \[\begin{aligned} g_1 &< 0 \\ \lambda_1 &= 0 \\ L_x &= 2y - 12 - \lambda_2 = 0 \\ L_y &= 6y - 4 = 0 \\ y &= 2/3 \\ \lambda_2 &= -32/3 < 0 \end{aligned}\]
  2. \[\begin{aligned} g_2 &< 0 \\ \lambda_2 &= 0 \\ L_x &= 6x + 2y - 12 + 2 \lambda_1 - \lambda_3 = 0 \\ L_y &= 2x + 6y - 4 + \lambda_1 - \lambda_3 = 0 \end{aligned}\]
    1. \[\begin{aligned} g_3 &= 0 \\ y &= -x \\ g_1 &= x - 1 \\ g_2 &= -x \\ L_x &= 4x - 12 + 2 \lambda_1 - \lambda_3 = 0 \\ L_y &= -4x - 4 + \lambda_1 - \lambda_3 = 0 \end{aligned}\]
      1. \[\begin{aligned} g_1 &= 0 \\ x &= 1 \\ g_2 &= -1 < 0 \\ L_x &= -8 + 2 \lambda_1 - \lambda_3 = 0 \\ L_y &= -8 + \lambda_1 - \lambda_3 = 0 \\ L_x - L_y &= \lambda_1 = 0 \\ \lambda_3 &= -8 < 0 \end{aligned}\]
      2. \[\begin{aligned} g_1 &< 0 \\ \lambda_1 &= 0 \\ L_x &= 4x - 12 - \lambda_3 = 0 \\ L_y &= -4x - 4 - \lambda_3 = 0 \\ L_x + L_y &= -16 - 2\lambda_3 = 0 \\ \lambda_3 &= -8 < 0 \end{aligned}\]
    2. \[\begin{aligned} g_3 &< 0 \\ \lambda_3 &= 0 \\ L_x &= 6x + 2y - 12 + 2 \lambda_1 = 0 \\ L_y &= 2x + 6y - 4 + \lambda_1 = 0 \end{aligned}\]
      1. \[\begin{aligned} g_1 &= 0 \\ y &= -2x + 1 \\ L_x &= 2x - 10 + 2 \lambda_1 = 0 \\ L_y &= -10x + 2 + \lambda_1 = 0 \\ 5 L_x + L_y &= -48 + 11 \lambda_1 = 0 \\ \lambda_1 &= 48/11 \ge 0 \\ L_x - 2 L_y &= 22x - 14 = 0 \\ x &= 7/11 \\ y &= -3/11 \\ g_2 &= -7/11 < 0 \\ g_3 &= -7/11 + 3/11 = -4/11 < 0 \end{aligned}\]

Optimalna vrednost: $(x, y) = (7/11, -4/11)$

Naloga 4

Poišči optimalno rešitev problema vezanih ekstremov z neenačbami

\[\begin{aligned} \min \quad x^2 -4x + y^2 -6y &+ 8 \\[1ex] x^2 - x + y^3 + \ln y &\le 1 \\ -2y + 1 &\le 0 \\ x + 2y &\le 3 \ . \end{aligned}\]

Namig: v optimalni rešitvi sta dva pogoja izpolnjena z enačajem.

\[\begin{aligned} f &= x^2 -4x + y^2 -6y + 8 & \text{konveksna} \\ g_1 &= x^2 - x + y^3 + \ln y - 1 \\ g_2 &= -2y + 1 & \text{linearna } (y \ge 1/2) \\ g_3 &= x + 2y - 3 & \text{linearna} \\ H_f &= \begin{pmatrix} 2 & 0 \\ 0 & 2 \end{pmatrix} \ge 0 \\ H_{g_1} &= \begin{pmatrix} 2 & 0 \\ 0 & 6y - {1 \over y^2} \end{pmatrix} \ge 0 &\text{če } y \ge \sqrt[3]{1/6} > 1/2 \end{aligned}\]

Nismo uspeli dokazati, da je območje, omejeno z ${g_1}, {g_2}, {g_3}$, konveksno!

Ta stran je odprtokodna. Izboljšaj to stran.
Ta zapisek je dostopen tudi na HackMD.