Optimizacijske metode
Optimizacijske metode - vaje 2.4.2021
Problem razvoza
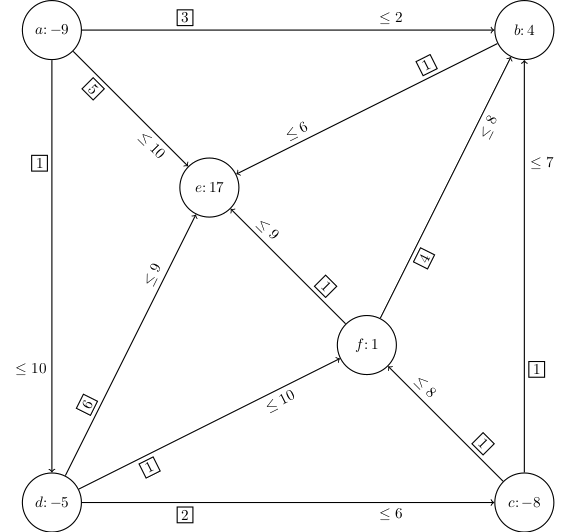
Naloga 1
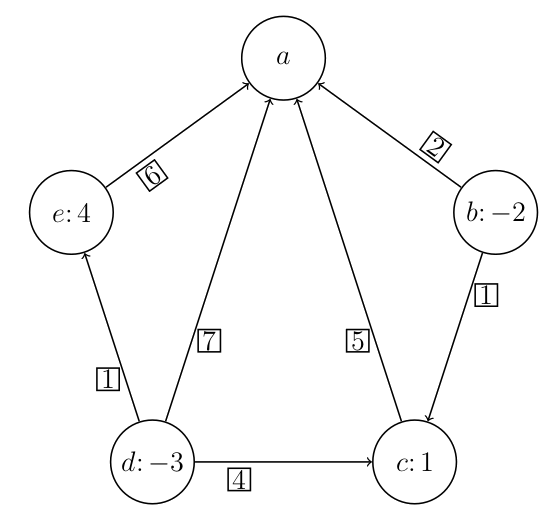
Reši problem razvoza na grafu s simpleksno metodo za omrežje v odvisnosti od parametra $\alpha$.
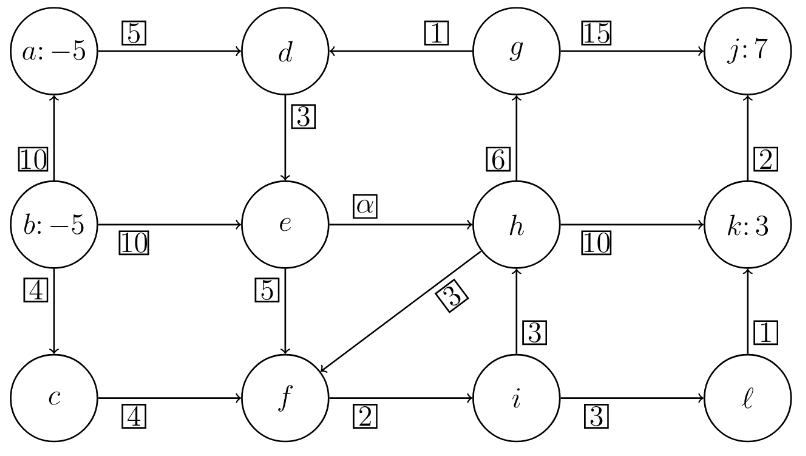
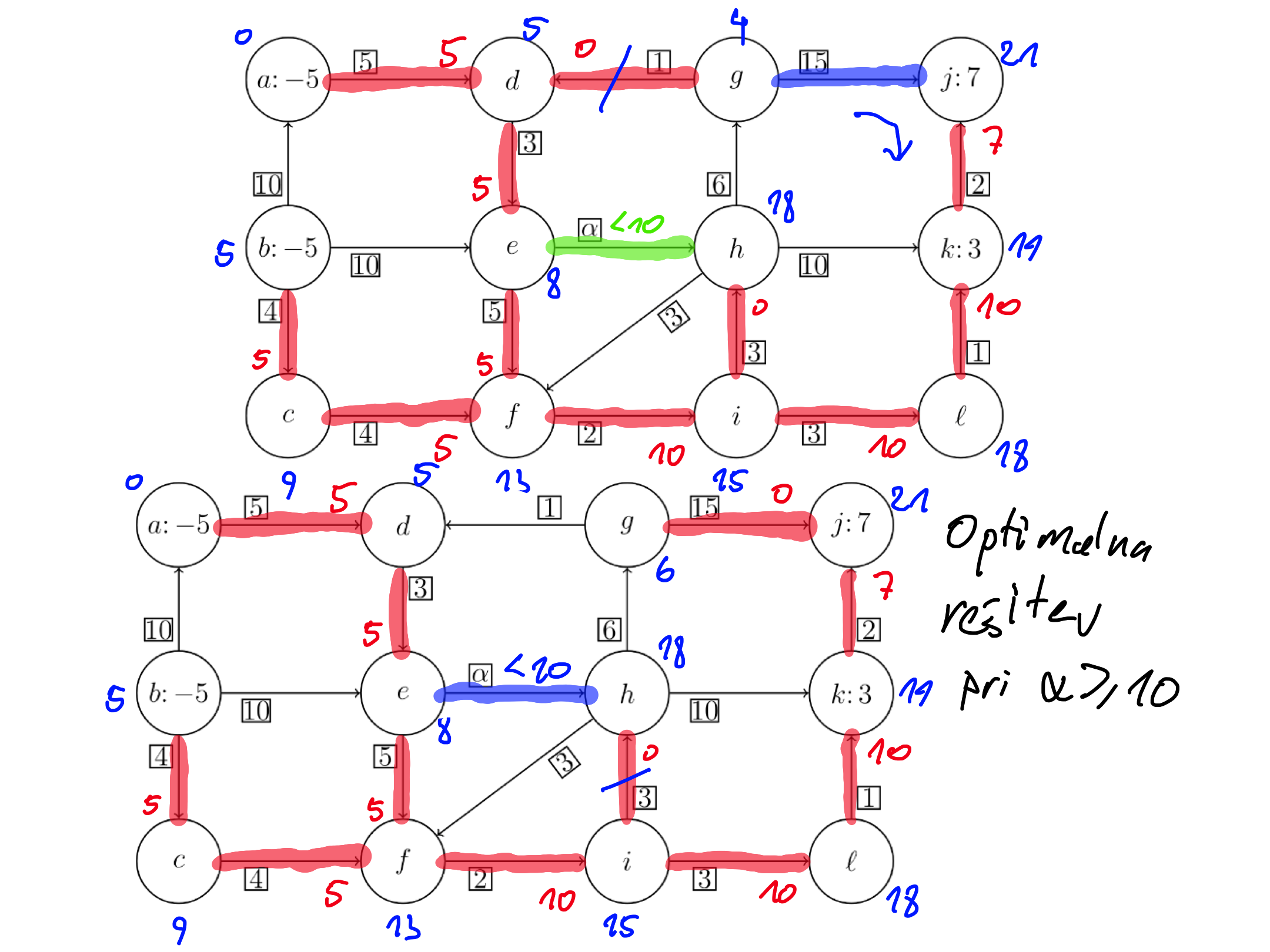
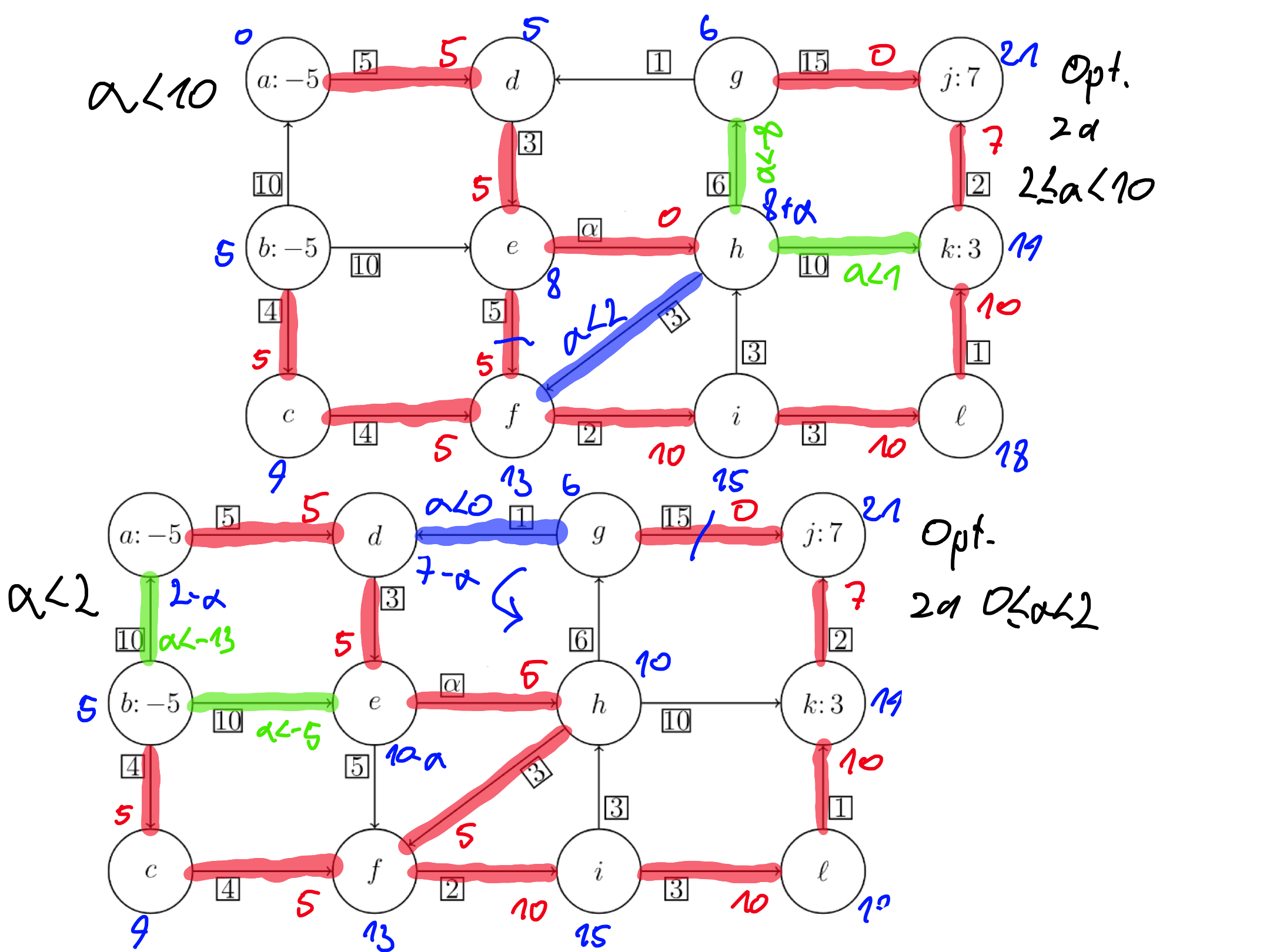

Naloga 2
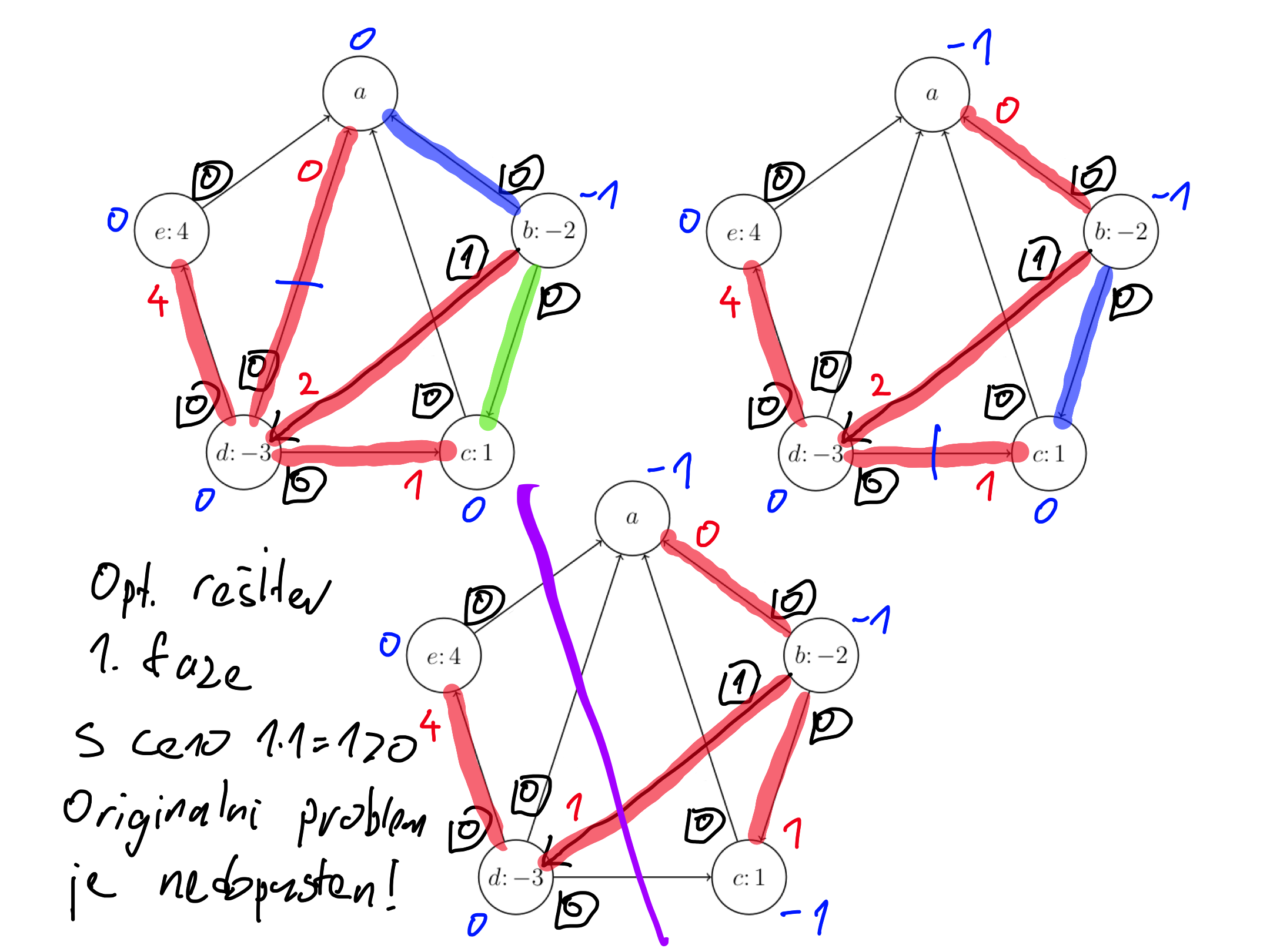
Pokaži, da problem razvoza nima dopustne rešitve.
Naloga 3
S pomočjo dualnosti dokaži optimalnost podanega razvoza.
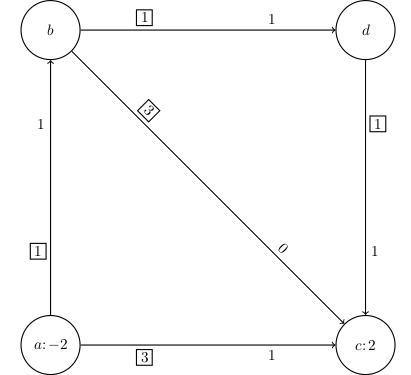
\[\begin{aligned} \min \ x_{ab} + 3 x_{ac} + 3 x_{bc} + x_{bd} + x_{dc} \\[1ex] -x_{ab} - x_{ac} &= -2 & a \\ x_{ab} - x_{bc} - x_{bd} &= 0 & b \\ x_{ac} + x_{bc} + x_{dc} &= 2 & c \\ x_{bd} - x_{dc} &= 0 & d \\[1ex] x_{ab}, x_{ac}, x_{bc}, x_{bd}, x_{dc} &\ge 0 \end{aligned}\]
Dual:
\[\begin{aligned} \max \ -2 y_a + 2 y_c \\[1ex] -y_a + y_b &\le 1 \\ -y_a + y_c &\le 3 \\ -y_b + y_c &\le 3 \\ -y_b + y_d &\le 1 \\ y_c - y_d &\le 1 \end{aligned}\]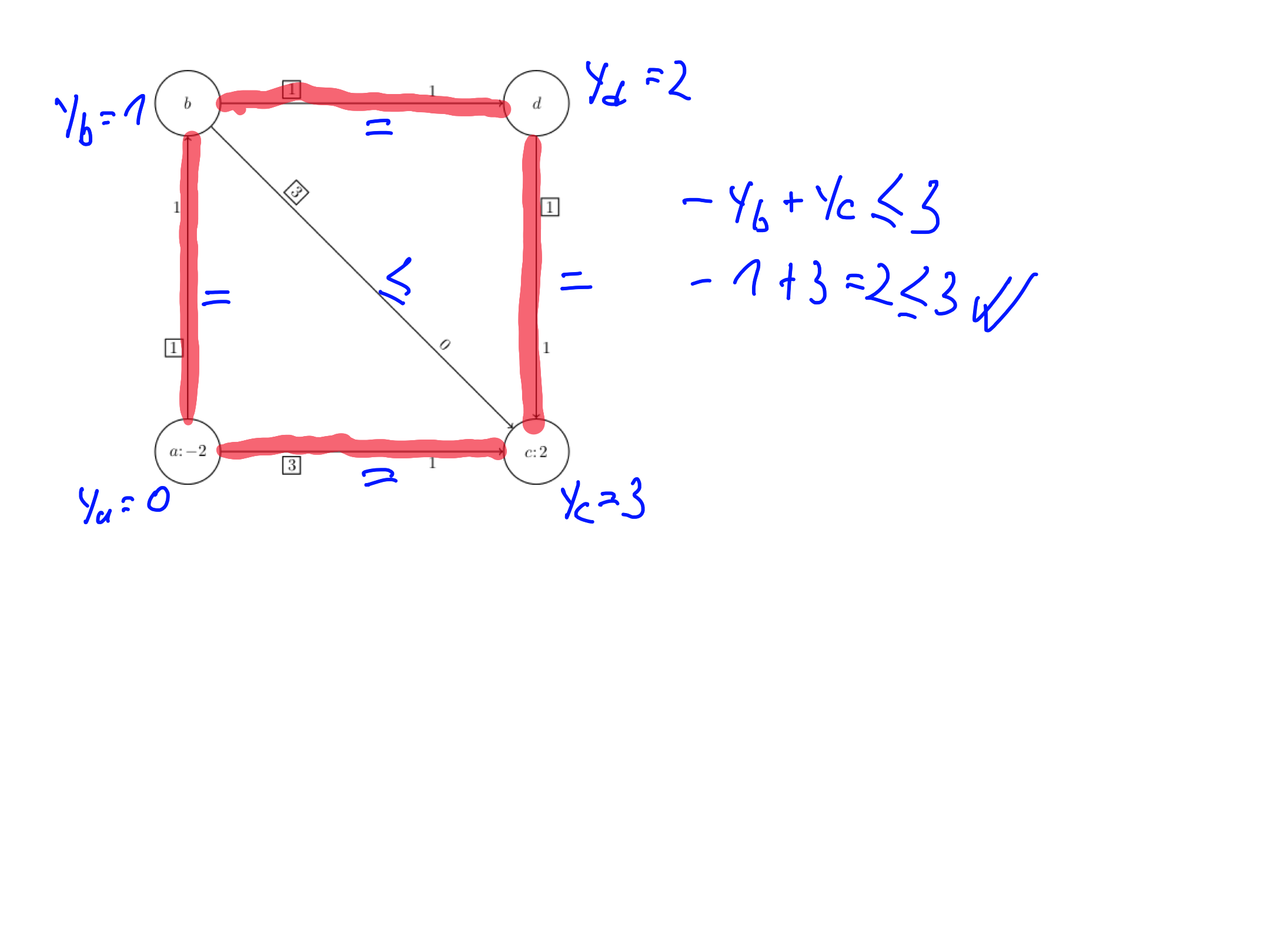
Naloga 4
Poišči najcenejši razvoz na sledečem grafu.
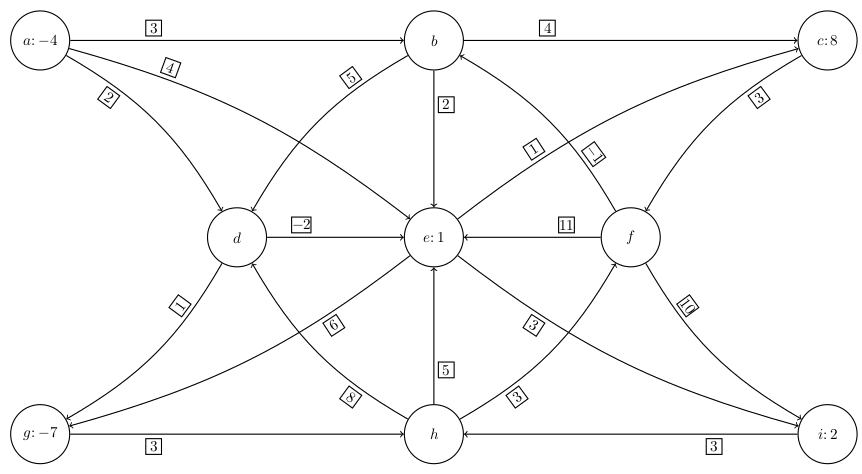
Naloga 5
Reši problem razvoza na grafu z omejitvami.