Optimizacijske metode
Optimizacijske metode - vaje 26.3.2021
Problem razvoza
Naloga 1
Reši problem razvoza na grafu s simpleksno metodo za omrežje.
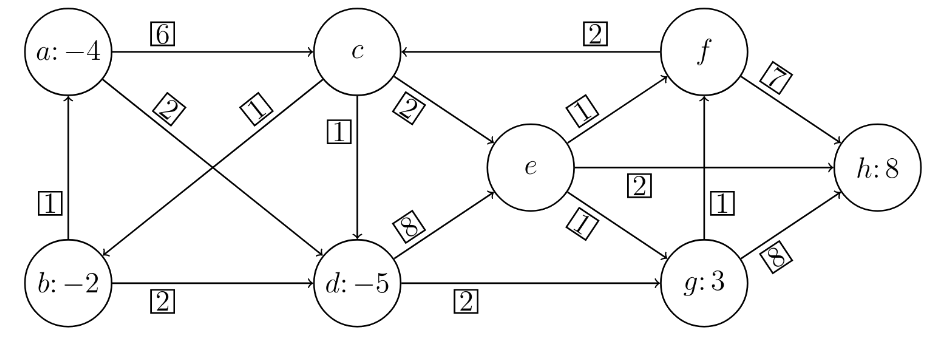
Najprej poiščemo dopustno rešitev:

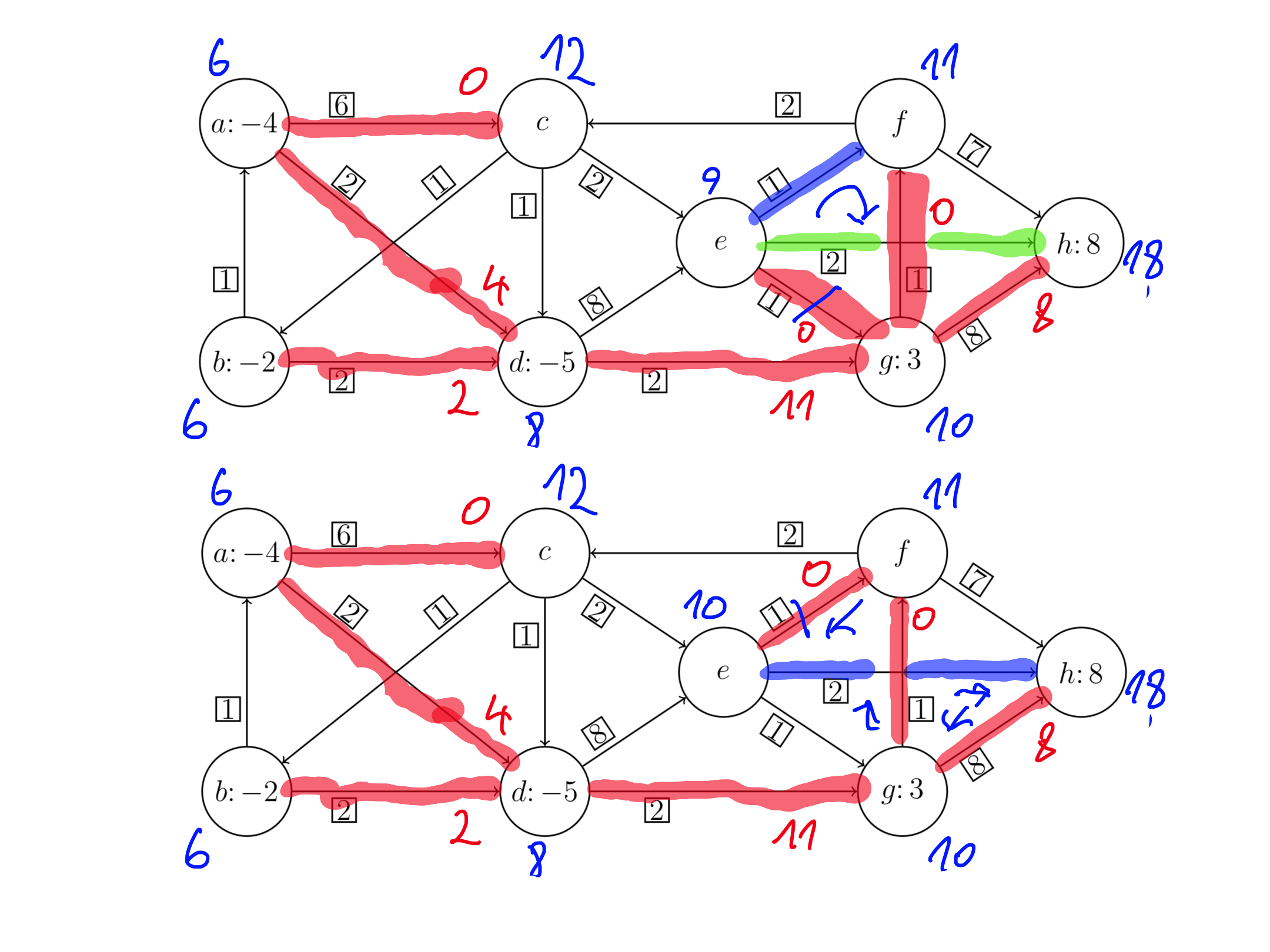
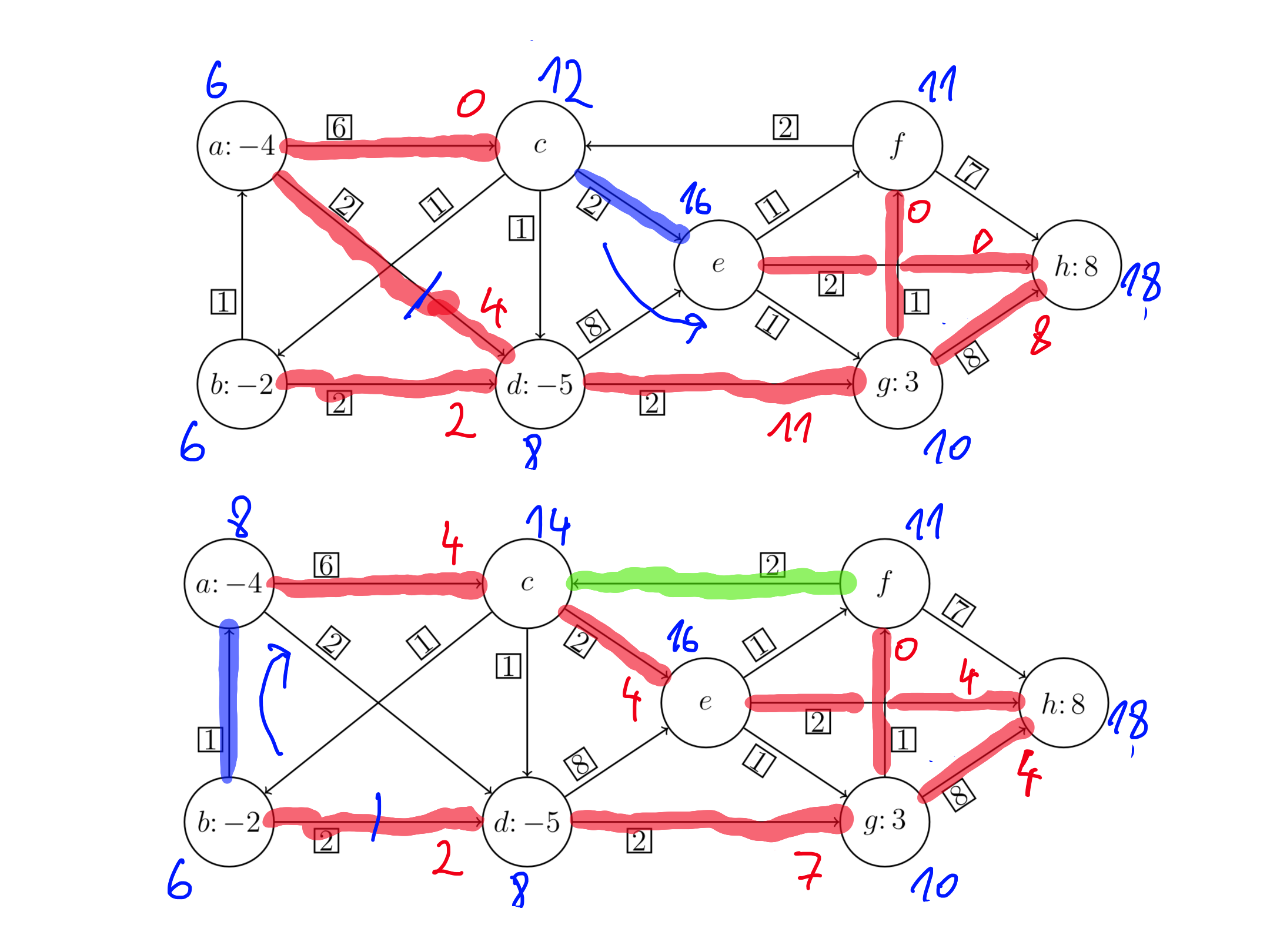

Cena razvoza: $2 \cdot 1 + 6 \cdot 6 + 8 \cdot 2 + 8 \cdot 2 + 5 \cdot 2 + 2 \cdot 1 + 2 \cdot 2 = 86$
Po povezavi $bd$ bi lahko povečali prepeljano količino za $x \in [0, 2]$ (omejuje nas povezava $ba$) in tako dobili splošno optimalno rešitev.
Naloga 2
Reši problem razvoza na grafu s simpleksno metodo za omrežje. Pazi na skupno povpraševanje in ponudbo!
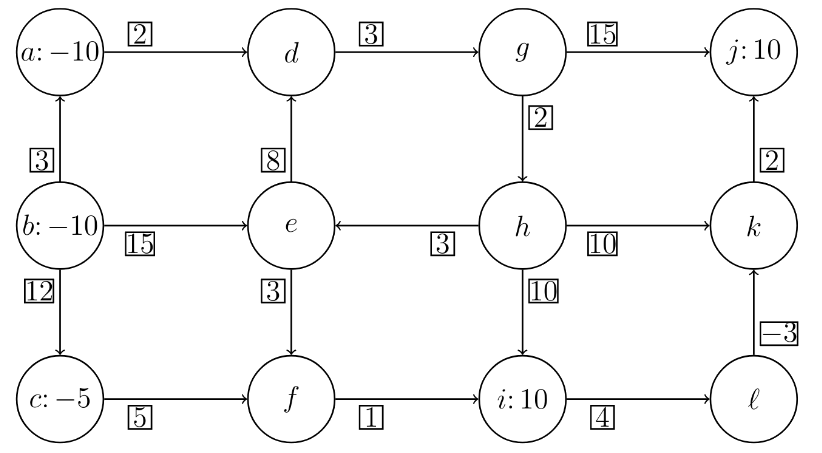
Ker je ponudba večja od povpraševanja, graf dopolnimo z novim vozliščem.
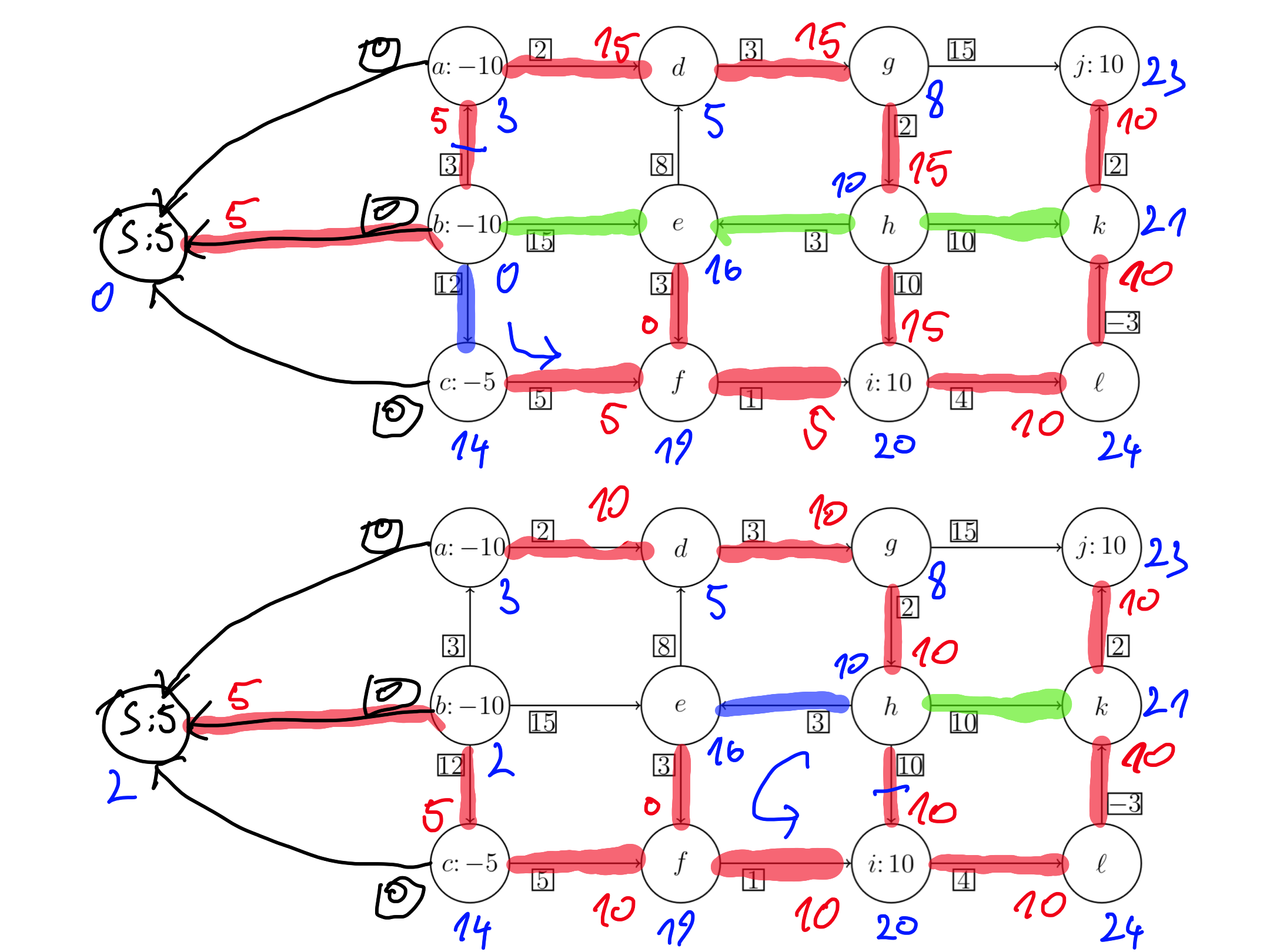

Cena razvoza: $5 \cdot 0 + 5 \cdot 3 + 15 \cdot 2 + 15 \cdot 3 + 15 \cdot 2 + 15 \cdot 3 + 15 \cdot 3 + 5 \cdot 5 + 20 \cdot 1 + 10 \cdot 4 + 10 \cdot (-3) + 10 \cdot 2 = 285$
Naloga 3
Reši problem razvoza na grafu z dvofazno simpleksno metodo za omrežje.
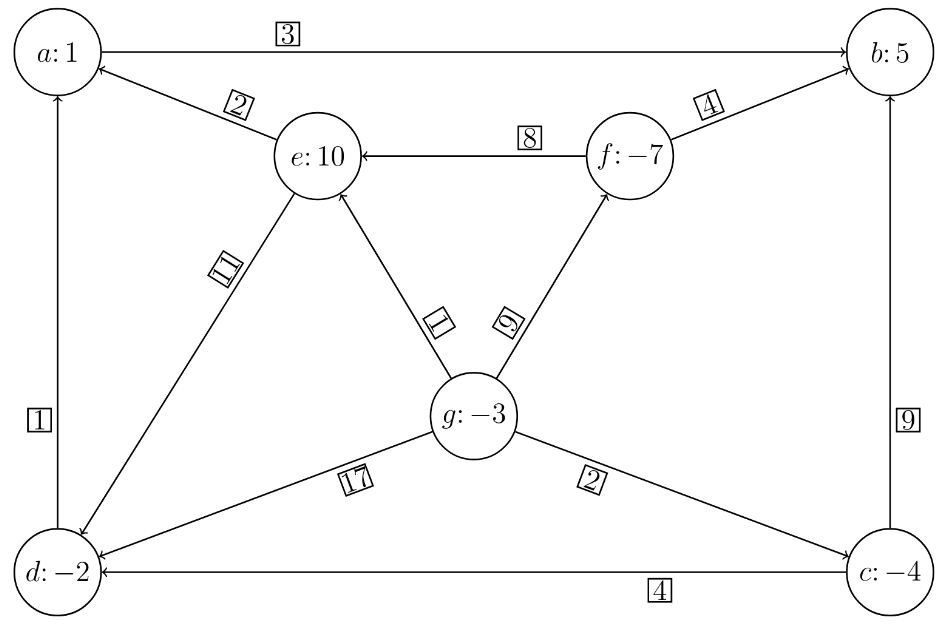
Sestavimo omrežje prve faze, da poiščemo začetno dopustno rešitev.
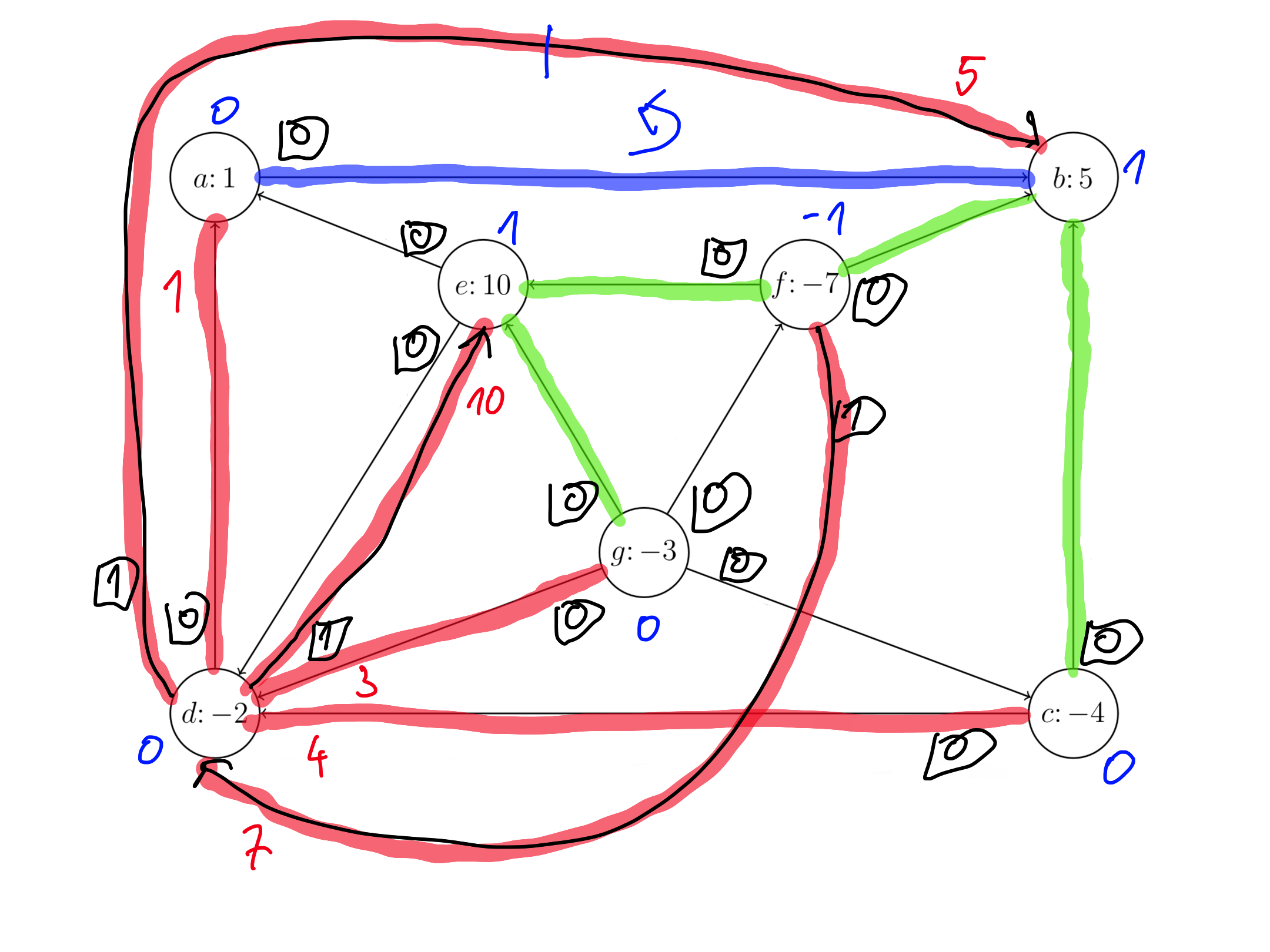

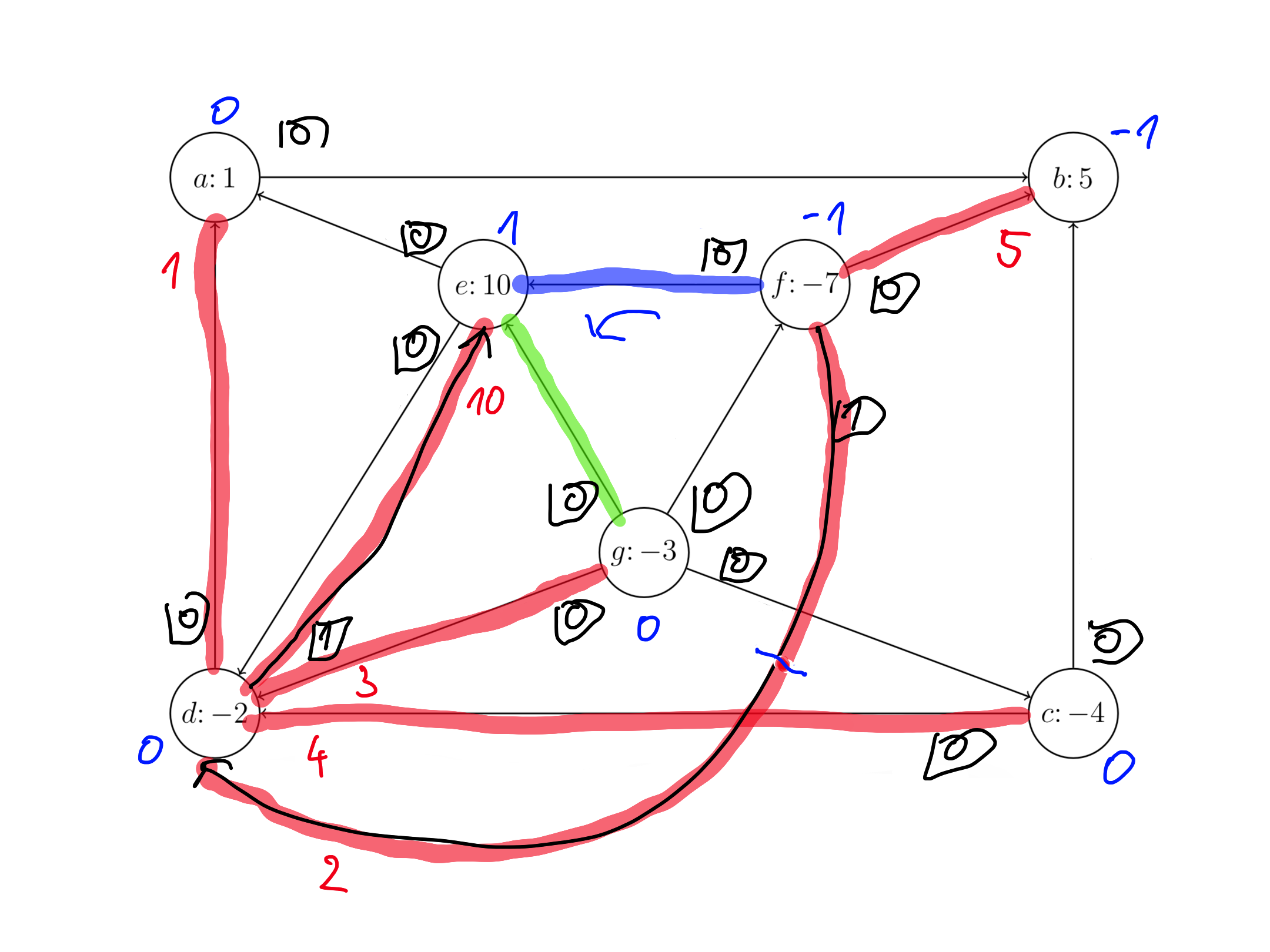
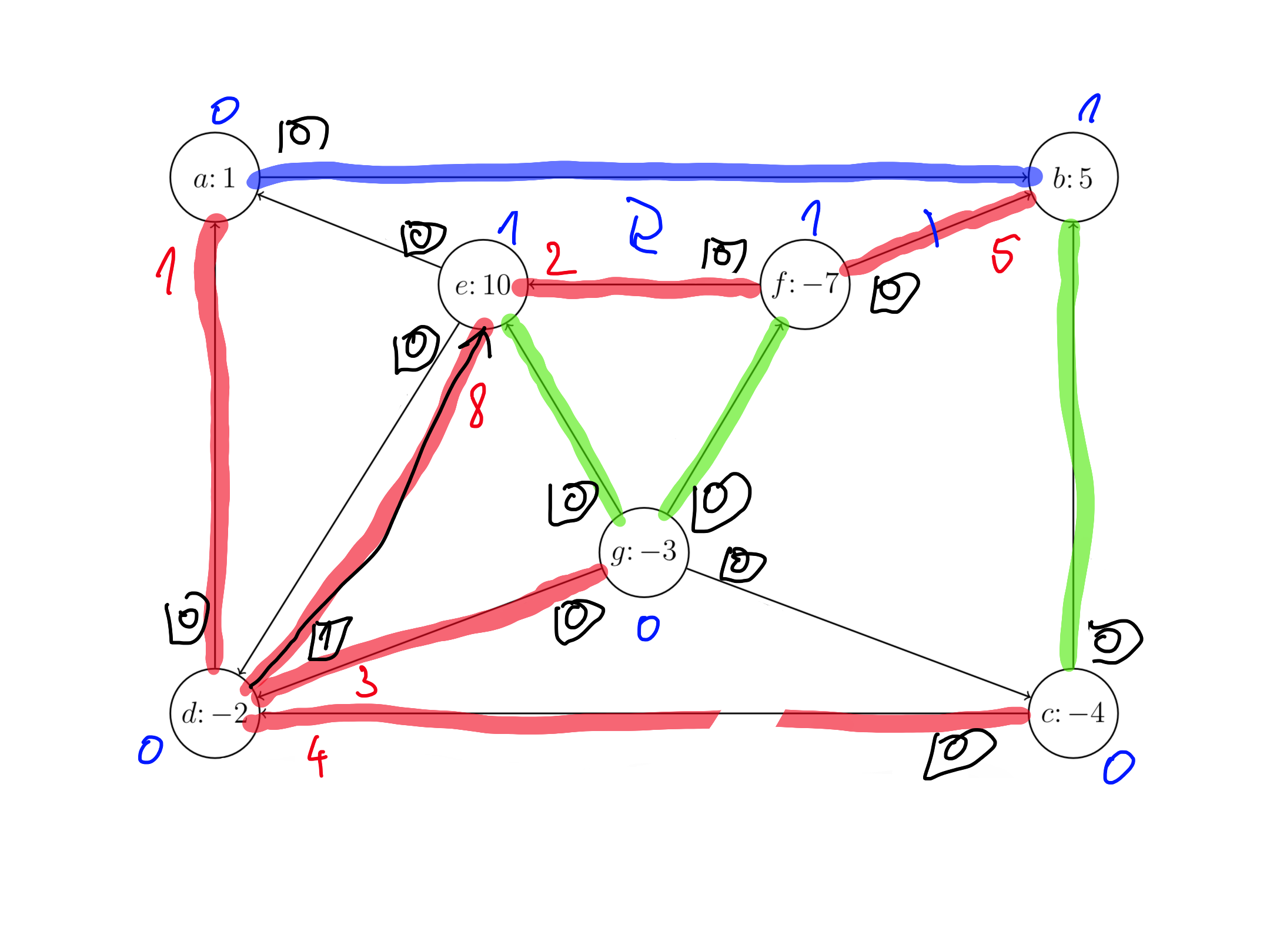
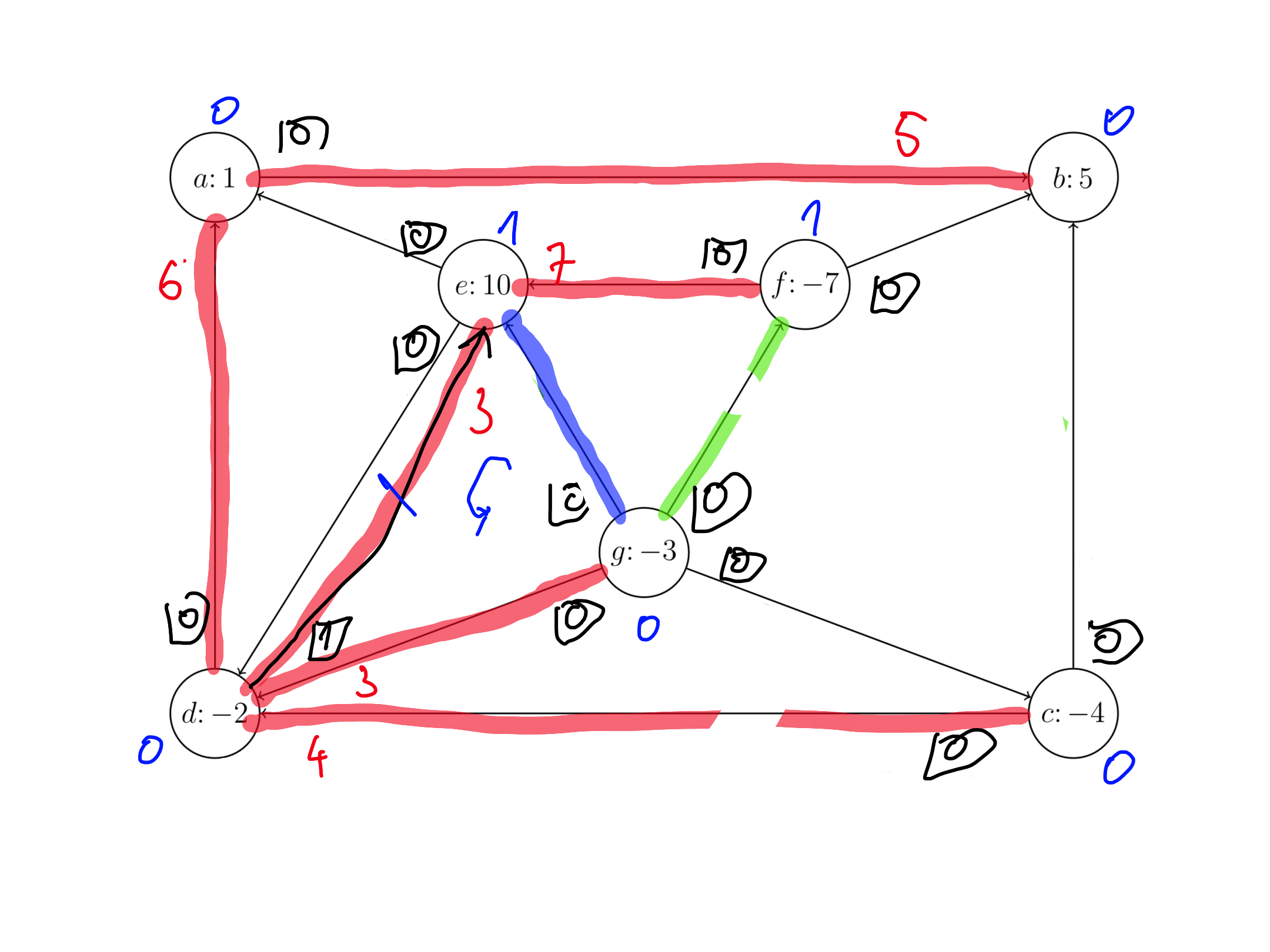
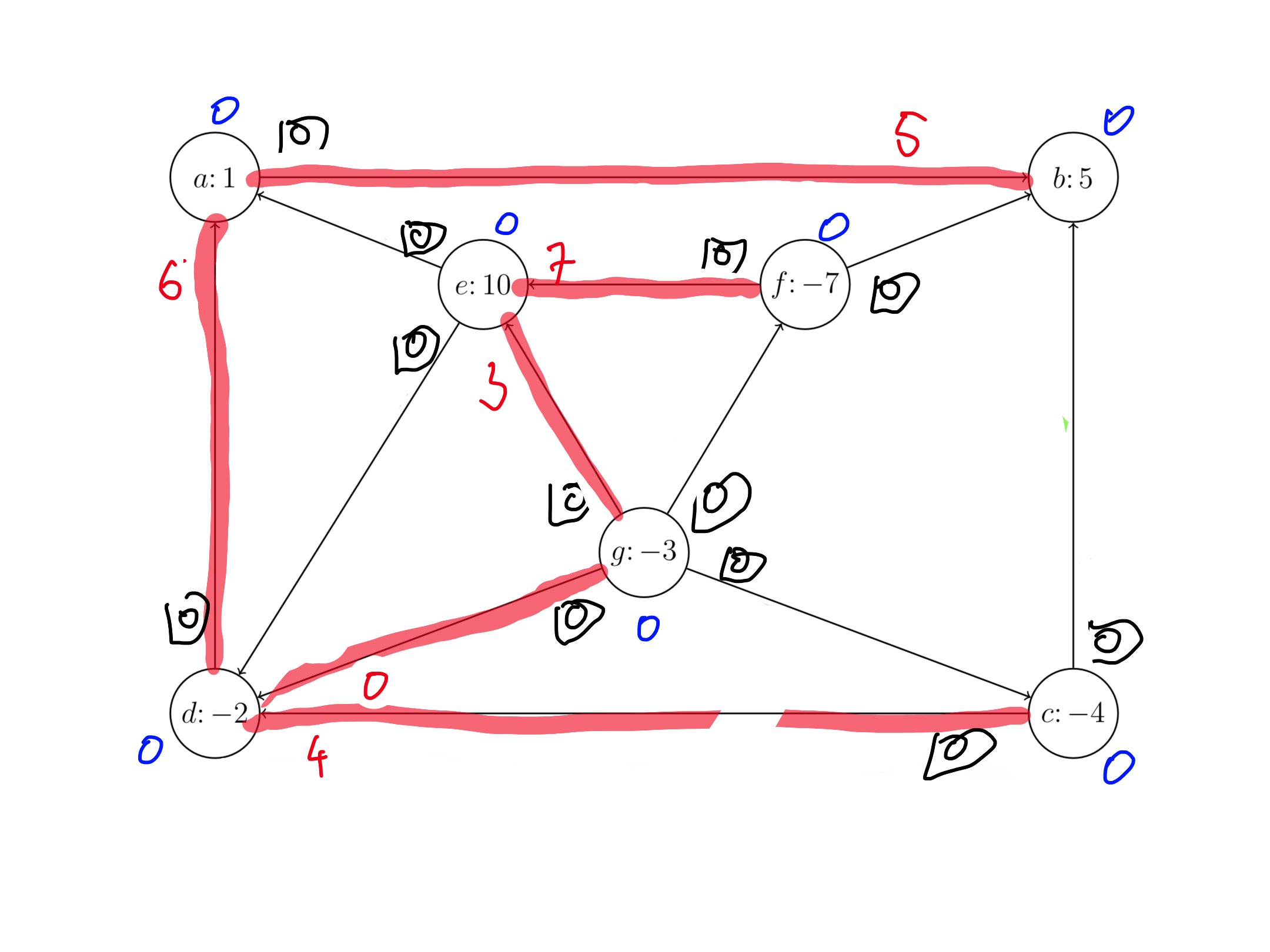
Našli smo optimalno rešitev prve faze, uporabimo dobljeno drevo kot dopustno rešitev originalnega problema.
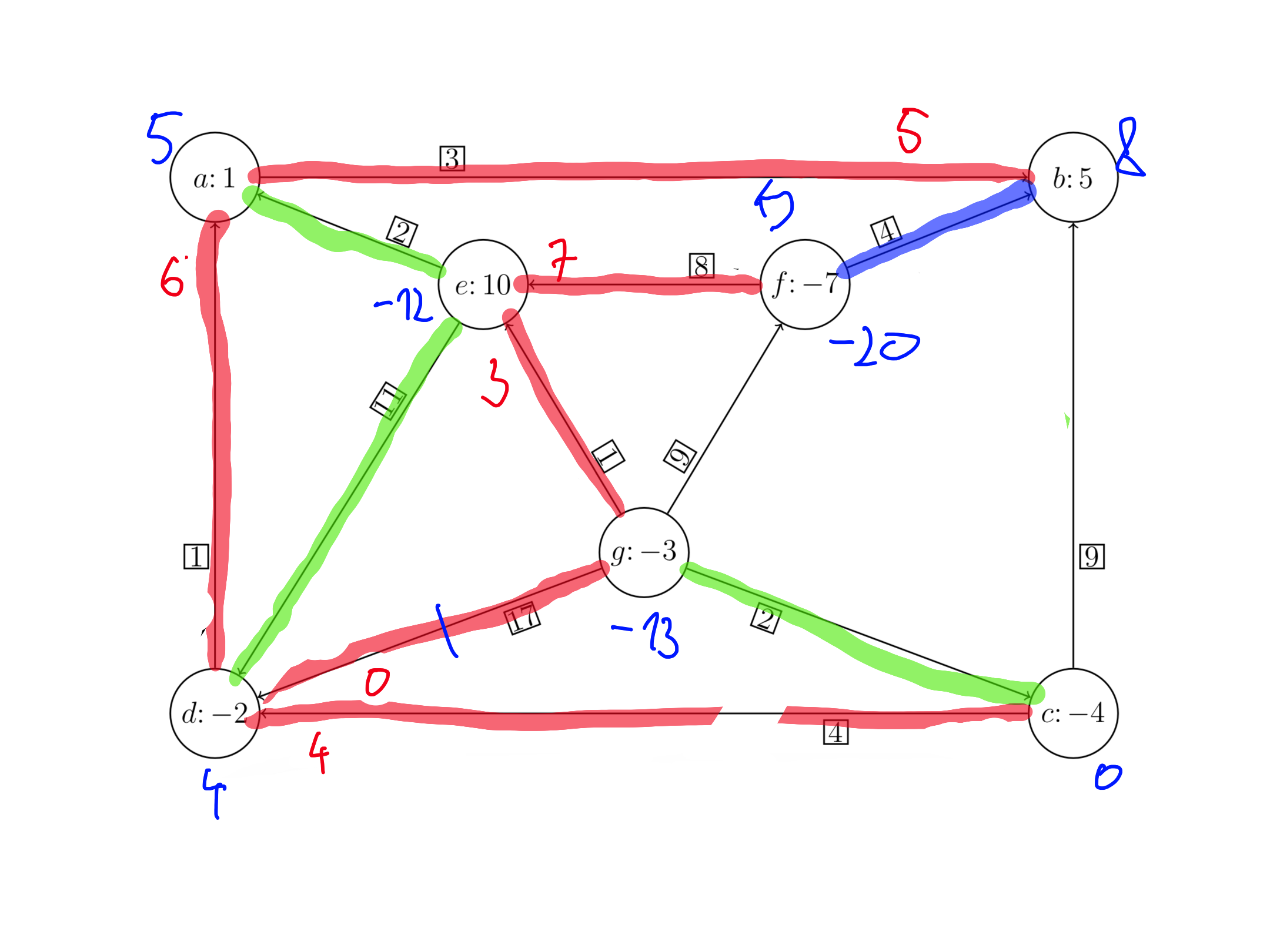

Cena razvoza: $4 \cdot 4 + 6 \cdot 1 + 3 \cdot 5 + 3 \cdot 1 + 8 \cdot 7 + 4 \cdot 0 = 96$