Operacijske raziskave
Operacijske raziskave - vaje 17.5.2021
Floyd-Warshallov algoritem
class UtezenDigraf(Digraf):
...
def floydWarshall(G):
razdalja = {(u, v): 0 if u == v else float('inf')
for u in G.vozlisca() for v in G.vozlisca()}
stars = {(u, v): None for u in G.vozlisca() for v in G.vozlisca()}
for u in G.vozlisca():
for v, r in G.utezeniSosedi().items():
razdalja[u, v] = r
stars[u, v] = u
for w in G.vozlisca():
for u in G.vozlisca():
if razdalja[u, w] + razdalja[w, u] < 0:
raise ValueError("graf ima negativen cikel")
for v in G.vozlisca():
r = razdalja[u, w] + razdalja[w, v]
if r < razdalja[u, v]:
razdalja[u, v] = r
stars[u, v] = stars[w, v]
return (razdalja, stars)
Časovna zahtevnost: $O(n^3)$
- Dijkstrov algoritem (s kopico) iz vsakega vozlišča posebej: $O(mn \log n)$ je hitrejši, če velja $m = o(n^2/\log n)$ in nimamo negativnih uteži
Naloga 1
S pomočjo Floyd-Warshallovega algoritma poišči najkrajše poti med vsemi pari vozlišč.

| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 3/A | 10/B | 3/C | 12/B | 1/G | 2/H | 7/D |
| B | 0 | 7/B | 0/C | 9/B | -2/G | -1/H | 4/D | |
| C | 2/D | 0 | -7/C | 11/B | -3/G | -8/H | -3/D | |
| D | 9/D | 16/B | 0 | 18/B | -2/G | -1/H | 4/D | |
| E | 10/D | 17/B | 1/E | 0 | -1/G | 0/H | 5/D | |
| F | 0 | 8/F | ||||||
| G | -1/G | 0 | ||||||
| H | -6/G | -5/H | 0 |
Uporaba algoritmov na grafih
Naloga 2
Denimo, da imamo neusmerjen graf $G = (V, E)$, katerega vozlišča predstavljajo mesta, povezave pa predstavljajo ceste, ki jih povezujejo. Za vsako povezavo $e \in E$ poznamo njeno dolžino ${\ell_e}$ (v kilometrih).
Priti želimo iz mesta $s$ v mesto $t$. V vsakem mestu je bencinska črpalka, ob cestah pa teh ni. Žal imamo na voljo samo star avto, ki lahko s polnim rezervoarjem prepelje le $L$ kilometrov.
- Zapiši algoritem, ki v linearnem času poišče pot, ki jo lahko prevozimo z našim avtom, oziroma ugotovi, da ta ne obstaja.
- Izkaže se, da z našim avtom te poti ne moremo prevoziti, zato se odločimo za nakup novega. Zapiši algoritem, ki v času $O(m \log n)$ določi najmanjše število prevoženih kilometrov, ki naj jih avto zmore z enim polnjenjem, da bo pot od $s$ do $t$ mogoča.
-
- Konstruiramo graf $G’ = (V, E’)$, kjer je $E’ = \lbrace e \in E \mid {\ell_e} \le L \rbrace$
- Uporabimo BFS ali DFS na $G’$ z začetkom v $s$
- Če dosežemo vozlišče $t$, potem ustrezna pot obstaja
- Časovna zahtevnost: $O(m)$
- Varianta Dijkstrovega algoritma:
def minPrevozenih(G, s, t): Q = Kopica({v: -float('inf') if v == s else float('inf') for v in G.vozlisca()}) min_prevozenih = {} stars = {s: None} while len(Q) > 0: v, d = Q.pop() min_prevozenih[v] = d if v == t: return (min_prevozenih[t], stars) for w, l in G.utezeniSosedi(v).items(): if w in min_prevozenih: continue r = max(d, l) if r < Q[w]: Q[w] = r stars[w] = v raise ValueError("končnega vozlišča ni mogoče doseči")
Naloga 3
Oviratlon je tekalna preizkušnja na 8 do 10 kilometrov dolgi poti z različnimi ovirami. Zanima nas, na koliko različnih načinov lahko pridemo od štarta do cilja. Dan je utežen usmerjen acikličen graf $G$ ter vozlišči $s$ in $t$, ki predstavljata štart oziroma cilj. Uteži na povezavah nam predstavljajo, na koliko načinov jih lahko prečkamo.
-
Reši nalogo za sledeči graf.
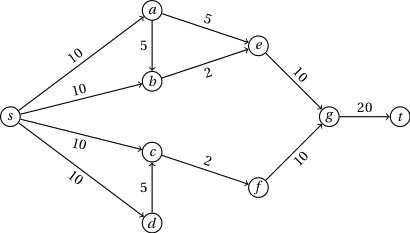
-
Zapiši algoritem, ki reši dani problem. Kakšna je njegova časovna zahtevnost?
def oviratlon(G, s, t):
nacini = {v: 1 if v == s else 0 for v in G.vozlisca()}
for u in G.topoloskoUrejanje():
for v, st in G.utezeniSosedi(u).items():
nacini[v] += nacini[u] * st
return nacini[t]
Časovna zahevnost: $O(m)$
| s | a | b | d | c | e | f | g | t |
|---|---|---|---|---|---|---|---|---|
| 1 | 10 | 60 | 10 | 60 | 170 | 120 | 2900 | 58000 |
Naloga 4
Dan je neusmerjen utežen graf $G = (V, E)$ z nenegativnimi cenami povezav ${L_e}$ ($e \in E$). Naj bosta $A$ in $B$ disjunktni množici povezav, tako da velja $E = A \cup B$. Želimo najti najcenejšo alternirajočo pot med danima vozliščema $s, t \in V$ - torej takšno, v kateri se povezave iz $A$ in iz $B$ izmenjujejo (ni pomembno, ali začnemo oziroma končamo s povezavo iz množice $A$ ali $B$). Posamezno vozlišče se lahko v alternirajoči poti pojavi tudi večkrat.
-
Predlagaj čim učinkovitejši algoritem za reševanje danega problema. Kakšna je njegova časovna zahtevnost?
Namig: grafu $G$ priredi usmerjen graf $G’$, v katerem bodo vse poti od $s$ do $t$ ustrezale alternirajočim potem v $G$. Po potrebi lahko vozlišča tudi podvojiš.
-
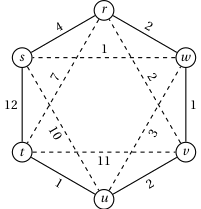
S svojim algoritmom poišči najcenejšo alternirajočo pot od $s$ do $t$ na spodnjem grafu. Povezave iz množice $A$ so označene s polno, povezave iz množice $B$ pa s črtkano črto. Iz rešitve naj bo jasno, kako poteka izvajanje algoritma.