Operacijske raziskave
Operacijske raziskave - vaje 23.3.2020
Odločitvena drevesa
Naloga 1
Imaš sledeče odločitveno drevo, a nisi prepričan glede vrednosti $p \in [0, 1/3]$. Poišči optimalne odločitve glede na vrednost $p$. Pričakovano vrednost želimo maksimizirati.
graph LR
A[A] -- p < 5/19 --- B[B]
A -- p >= 5/19 --- C([C: 22p-5])
B -- p > 2/7 --- D([D: 10p-2])
B == p <= 2/7 === E([E: 3p])
C -- p --- F>10]
C -- p --- G>2]
C -- 1-2p --- H>-5]
D -- 2p --- I>3]
D -- 1-2p --- J>-2]
E -- 3p --- K>1]
E -- 1-3p --- L>0]
\[\begin{alignedat}{2} E(D) &= 2p \cdot 3 + (1-2p) \cdot (-2) &&= 10p - 2 \\ E(E) &= 3p \cdot 1 + (1-3p) \cdot 0 &&= 3p \\ E(C) &= p \cdot 10 + p \cdot 2 + (1-2p) \cdot (-5) &&= 22p - 5 \end{alignedat}\] \[\begin{aligned} 10p - 2 &> 3p \\ 7p &> 2 \\ p &> 2/7 \end{aligned}\] \[E(B) = \begin{cases} 10p - 2 & p > 2/7 \\ 3p & p \le 2/7 \end{cases}\] \[\begin{aligned} 3p &> 22p - 5 \\ 19p &< 5 \\ p &< 5/19 < 2/7 \end{aligned}\] \[\begin{aligned} 10p - 2 &> 22p - 5 \\ 12p &< 3 \\ p &< 1/4 < 2/7 \end{aligned}\] \[E(A) = \begin{cases} 3p & p < 5/19 \\ 22p - 5 & p \ge 5/19 \end{cases}\]
Naloga 2
Pacient ima na voljo operacijo. Brez operacije bo živel natanko $3$ mesece. Z uspešno opravljeno operacijo bo živel natanko $12$ mesecev. Operacija je neuspešna z verjetnostjo $0.3$ (v tem primeru pacient dočaka $0$ mesecev). Cilj pacienta je maksimiranje pričakovane življenjske dobe.
- Ali naj pacient sprejme operacijo?
- Pacient lahko opravi predhodni test, ki z zanesljivostjo $0.9$ napove uspešnost operacije, vendar z verjetnostjo $0.005$ pacient zaradi komplikacij med testom umre. Ali naj pacient opravi test?
Nariši odločitveno drevo in odločitve sprejmi na podlagi izračunanih verjetnosti!
\[\begin{aligned} X &\dots \text{čas življenja} \\ A &\dots \text{operacija uspešna} \\ B &\dots \text{sprejme operacijo} \\ C &\dots \text{opravi test} \\ D &\dots \text{test poztiven} \\ E &\dots \text{komplikacije} \end{aligned}\] \[\begin{aligned} P(A) &= 0.7 \\ P(\lnot A) &= 0.3 \\[1ex] E(X \mid \lnot C \land \lnot B) &= 3 \\ E(X \mid \lnot C \land B \land A) &= 12 \\ E(X \mid \lnot C \land B \land \lnot A) &= 0 \\[1ex] E(X \mid \lnot C \land B) &= 0.7 \cdot 12 + 0.3 \cdot 0 = 8.4 \\[1ex] P(D \mid A) &= 0.9 \\ P(\lnot D \mid A) &= 0.1 \\ P(\lnot D \mid \lnot A) &= 0.9 \\ P(D \mid \lnot A) &= 0.1 \\[1ex] P(E \mid C) &= 0.005 \\[1ex] P(D) &= 0.9 \cdot 0.7 + 0.1 \cdot 0.3 = 0.66 \\ P(\lnot D) &= 0.1 \cdot 0.7 + 0.9 \cdot 0.3 = 0.34 \end{aligned}\] \[\begin{alignedat}{3} P(A \mid D) &= {P(D \mid A) \cdot P(A) \over P(D)} &&= {0.9 \cdot 0.7 \over 0.66} &&\approx 0.955 \\ P(\lnot A \mid D) &= {P(D \mid \lnot A) \cdot P(\lnot A) \over P(D)} &&= {0.1 \cdot 0.3 \over 0.66} &&\approx 0.045 \\ P(A \mid \lnot D) &= {P(\lnot D \mid A) \cdot P(A) \over P(\lnot D)} &&= {0.1 \cdot 0.7 \over 0.34} &&\approx 0.206 \\ P(\lnot A \mid \lnot D) &= {P(\lnot D \mid \lnot A) \cdot P(\lnot A) \over P(\lnot D)} &&= {0.9 \cdot 0.3 \over 0.34} &&\approx 0.794 \end{alignedat}\]
graph LR
C[opravi test?: 8.537] == ja === E([komplikacije?: 8.537])
C -- ne --- B
E -- ja: 0.005 --- w>0]
E -- ne: 0.995 --- D([pozitiven?: 8.58])
D -- ja: 0.66 --- BD
D -- ne: 0.34 --- BC
BD[sprejme?: 11.455] == ja === AD([uspešna?: 11.455])
BD -- ne --- zD>3]
AD -- ja: 0.955 --- yD>12]
AD -- ne: 0.045 --- xD>0]
BC[sprejme?: 3] -- ja --- AC([uspešna?: 2.471])
BC == ne === zC>3]
AC -- ja: 0.206 --- yC>12]
AC -- ne: 0.794 --- xC>0]
B[sprejme?: 8.4] == ja === A([uspešna?: 8.4])
B -- ne --- z>3]
A -- ja: 0.7 --- y>12]
A -- ne: 0.3 --- x>0]
Pacient naj se odloči za testiranje - če to da pozitiven rezultat, naj se odloči za operacijo, sicer pa ne. Pričakovana življenjska doba je $8.537$ mesecev.
Naloga 3
Podjetje je razvilo produkt, za katerega je konkurenca pripravljena plačati $15 M€$. Če se odločijo samostojno prodajati produkt, jih vzpostavitev proizvodnje stane $6 M€$, za vsak uspešno prodan produkt pa dobijo $600 €$. Računajo, da bi z verjetnostjo $0.5$ investicija uspela in bi prodali $100000$ produktov, z verjetnostjo $0.5$ pa bi projekt propadel in bi prodali zgolj $10000$ produktov. Podjetje se lahko odloči tudi za neodvisno raziskavo trga. Ta stane $1 M€$, z verjetnostjo $2/3$ pa bo pravilno napovedala uspeh projekta (ne glede na to, ali bi ta uspel ali ne). Kako naj se podjetje odloči?
\[\begin{aligned} X &\dots \text{zaslužek} \\ A &\dots \text{opravijo raziskavo} \\ B &\dots \text{napove uspeh} \\ C &\dots \text{vzpostavijo proizvodnjo} \\ D &\dots \text{projekt uspešen} \end{aligned}\] \[\begin{aligned} E(X \mid \lnot A \land \lnot C) &= 15 M€ \\ E(X \mid A \land \lnot C) &= 14 M€ \\ E(X \mid \lnot A \land C \land D) &= 54 M€ \\ E(X \mid A \land C \land D) &= 53 M€ \\ E(X \mid \lnot A \land C \land \lnot D) &= 0 M€ \\ E(X \mid A \land C \land \lnot D) &= -1 M€ \\[1ex] P(D) &= 0.5 \\ P(\lnot D) &= 0.5 \\[1ex] P(B \mid D) &= 2/3 \\ P(\lnot B \mid D) &= 1/3 \\ P(B \mid \lnot D) &= 1/3 \\ P(\lnot B \mid \lnot D) &= 2/3 \\[1ex] P(B) &= 2/3 \cdot 0.5 + 1/3 \cdot 0.5 = 0.5 \\ P(\lnot B) &= 0.5 \\[1ex] P(D \mid B) &= 2/3 \cdot 0.5 / 0.5 = 2/3 \\ P(D \mid \lnot B) &= 1/3 \cdot 0.5 / 0.5 = 1/3 \end{aligned}\]
graph LR
A[raziskava?] -- ja --- B([napoved?: 26])
A == ne === C[proizvodnja?: 27]
B -- ja: 0.5 --- CB[proizvodnja?: 35]
B -- ne: 0.5 --- CnB[proizvodnja?: 17]
C == ja === D([uspešen?: 27])
C -- ne --- a>15]
CB == ja === DB([uspešen?: 35])
CB -- ne --- aB>14]
CnB == ja === DnB([uspešen?: 17])
CnB -- ne --- anB>14]
D -- ja: 0.5 --- b>54]
D -- ne: 0.5 --- c>0]
DB -- ja: 2/3 --- bB>53]
DB -- ne: 1/3 --- cB>-1]
DnB -- ja: 1/3 --- bnB>53]
DnB -- ne: 2/3 --- cnB>-1]
Naloga 4
Rexhep Bajrami bi se rad naslednja štiri leta ukvarjal s prodajo sadja in zelenjave (po štirih letih mu poteče delovna viza). Rad bi najel parcelo za stojnico, ki bo stala $6000 €$. Če je lokacija dobra, bo imel $12000 €$ dobička, če pa je lokacija slaba, bo imel le $3000 €$ dobička. Ocenjuje, da je z verjetnostjo $2/3$ lokacija dobra, z verjetnostjo $1/3$ pa slaba.
- Z odločitvenim drevesom opiši njegove možnosti in ugotovi, kako naj se odloči ter kakšen dobiček naj pričakuje.
- Za nasvet lahko vpraša znanca Seada, ki “ima nos” za tovrstne posle. Sead mu lahko da nasvet, a zanj zahteva $1200 €$. Dobro je znano, da ima Sead naslednje pogojne verjetnosti $P(\text{Seadovo mnenje} \mid \text{kakovost parcele})$:
| dobra | slaba | |
|---|---|---|
| priporoča | $2/3$ | $1/2$ |
| odsvetuje | $1/3$ | $1/2$ |
Ali naj vpraša Seada za nasvet? Kakšen je pričakovani dobiček?
\[\begin{aligned} X &\dots \text{dobiček} \\ A &\dots \text{vprašamo za mnenje} \\ B &\dots \text{priporoča} \\ C &\dots \text{najem} \\ D &\dots \text{dobra odločitev} \end{aligned}\] \[\begin{aligned} E(X \mid \lnot A \land \lnot C) &= 0 \\ E(X \mid A \land \lnot C) &= -1200 \\ E(X \mid \lnot A \land C \land D) &= 6000 \\ E(X \mid \lnot A \land C \land \lnot D) &= -3000 \\ E(X \mid A \land C \land D) &= 4800 \\ E(X \mid A \land C \land \lnot D) &= -4200 \\[1ex] P(B \mid D) &= 2/3 \\ P(\lnot B \mid D) &= 1/3 \\ P(B \mid \lnot D) &= 1/2 \\ P(\lnot B \mid \lnot D) &= 1/2 \end{aligned}\]
graph LR
A[vpraša za mnenje?] -- ja --- B([priporoča?: 1800])
A == ne === C[najame?: 3000]
B -- ja: 11/18 --- CB[najame?: 2345.45]
B -- ne: 7/18 --- CnB[najame?: 942.86]
C == ja === D([dobra odločitev?: 3000])
C -- ne --- a>0]
CB == ja === DB([dobra odločitev?: 2345.45])
CB -- ne --- aB>-1200]
CnB == ja === DnB([dobra odločitev?: 942.86])
CnB -- ne --- anB>-1200]
D -- ja: 2/3 --- b>6000]
D -- ne: 1/3 --- c>-3000]
DB -- ja: 8/11 --- bB>4800]
DB -- ne: 3/11 --- cB>-4200]
DnB -- ja: 4/7 --- bnB>4800]
DnB -- ne: 3/7 --- cnB>-4200]
Naloga 5
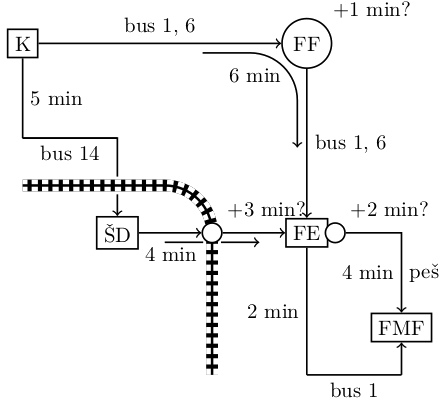
Mudi se ti na izpit, a ravno v trenutku, ko prideš na postajo Konzorcij, odpelje avtobus številka 1. Na prikazovalniku se izpiše, da bo naslednji avtobus številka 1 prispel čez $10$ minut, naslednji avtobus številka 6 čez $6$ minut, naslednji avtobus številka 14 pa čez $2$ minuti.
Avtobusa 1 in 6 ob ugodnih semaforjih potrebujeta $6$ minut do postaje pri FE, pri čemer se lahko čas vožnje zaradi rdeče luči na semaforju pri FF podaljša za $1$ minuto. Verjetnosti, da bo rdečo luč imel avtobus 1, da bo rdečo luč imel avtobus 6, ter da bosta oba avtobusa imela zeleno luč, so enake $1/3$ (zaradi majhnega razmaka se ne more zgoditi, da bi oba avtobusa naletela na rdečo luč). Avtobus številka 1 nadaljuje pot do postaje pri FMF, za kar potrebuje še $2$ minuti.
Avtobus številka 14 potrebuje $5$ minut do postaje pri študentskih domovih, od tam pa greš peš do postaje pri FE, za kar potrebuješ še $4$ minute. Pri tem prečkaš železnico – če mimo pripelje vlak (kar se zgodi z verjetnostjo $0.05$), se čas hoje podaljša za $3$ minute. Ko prideš na postajo pri FE (ne glede na to, ali si prišel z avtobusom 6 ali 14), te čakajo še $4$ minute hoje do FMF, vendar moraš najprej prečkati Tržaško cesto. Če je na semaforju rdeča luč (kar se zgodi z verjetnostjo 0.9, neodvisno od drugih dogodkov), se lahko odločiš, da $2$ minuti počakaš na zeleno luč in potem nadaljuješ peš, ali pa da greš nazaj do postaje in počakaš na avtobus številka $1$ (ki bo, tako kot prej, vozil še $2$ minuti do FMF).
Kakšne bodo tvoje odločitve, da bo pričakovano trajanje poti do FMF čim krajše? Nariši odločitveno drevo in odločitve sprejmi na podlagi izračunanih verjetnosti!