Diskretne strukture (FiM)

« nazaj

Diskretne strukture (FiM) - vaje 13.1.2021

---

Teorija grafov

• Graf je ravninski, če ga lahko vložimo v ravnino - tj., narišemo brez sekanja povezav.
• Graf ni ravninski, natanko tedaj ima minor ${K_5}$ ali ${K_{3, 3}}$ - do takega grafa lahko pridemo s krčenjem povezav ter odstranjevanjem povezav in vozlišč
• $v - e + f = 2$, kjer je $v$ število vozlišč, $e$ število povezav in $f$ število lic
  • velja za vložitve povezanih grafov v ravnino
  • za nepovezane grafe: $v - e + f = 1 +$ število povezanih komponent

---

Naloga 1

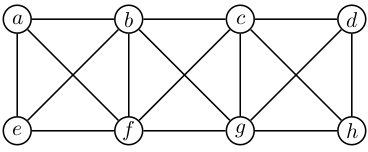
Za spodnje grafe ugotovi, ali so ravninski.

1. 
2. 
3. 
4. 

---

1. graph G1 {
     rankdir=LR
     a -- b -- c -- d -- h --g -- f
     a -- e -- f
     e -- b -- f -- c -- g -- d
     a -- f
     b -- g
     c -- h
   }
   

   Graf je ravninski.

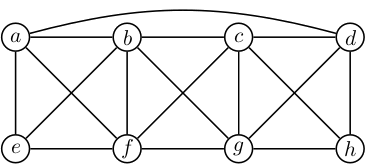
2. graph G2 {
     rankdir=LR
     node [style=filled]
        
     a [color=red]
     e [color=red]
     d [color=red]
     h [color=red]
     b [color=green]
     c [color=blue]
     f [color=yellow]
     g [color=magenta]
        
     a -- b -- c -- d
     d -- h  [color=red]
     h -- g -- f
     a -- e [color=red]
     e -- f
     e -- b -- f -- c -- g -- d
     a -- f
     b -- g
     c -- h
     a -- d  [color=red]
   }
   

   Graf ni ravninski, ima minor ${K_5}$:

   graph G2kontrakt {
     eadh -- b
     eadh -- c
     eadh -- f
     eadh -- g
     b -- c
     b -- f
     b -- g
     c -- f
     c -- g
     f -- g
   }
   

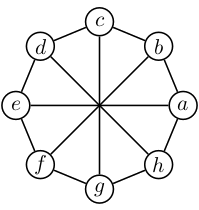
3. graph G3 {
     rankdir=LR
     node [style=filled]
        
     a [color=red]
     b [color=red]
     e [color=green]
     f [color=green]
     c [color=blue]
     d [color=cyan]
     g [color=magenta]
     h [color=yellow]
        
     a -- b [color=red]
     b -- c -- d -- e
     e -- f [color=green]
     f -- g -- h -- a
     a -- e
     b -- f
     c -- g
     d -- h
   }
   

   Graf ni ravninski, ima minor ${K_{3, 3}}$:

   graph G3kontrkat {
     ab -- c
     ab -- h
     ab -- ef
     d -- c
     d -- h
     d -- ef
     g -- c
     g -- h
     g -- ef
   }
   

---

Naloga 2

Pokaži, da ima povezan kubičen graf v ravnini, pri katerem so vsa lica petkotniki ali šestkotniki, natanko $12$ petkotnikov.

---

• $a$ število petkotnikov, $b$ število šestkotnikov
• $f = a + b$
• $3v = 2e = 5a + 6b$
• $v - e + f = 2$
• ${5a + 6b \over 3} - {5a + 6b \over 2} + a + b = 2$
• $-{5a + 6b \over 6} + a + b = 2$
• $a = 12$

---

Naloga 3

Naj bo $G$ enostaven graf, ki ima $11$ vozlišč. Pokaži, da potem $G$ ni ravninski ali pa njegov komplement ni ravninski.

---

• $v = 11$
• $e + \overline{e} = 55$
• Predpostavimo, da sta $G$ in $\overline{G}$ ravninska grafa.
• $v - e + f \ge 2$
• $v - \overline{e} + \overline{f} \ge 2$
• $2v - e - \overline{e} + f + \overline{f} \ge 4$
• $22 - 55 + f + \overline{f} \ge 4$
• $f + \overline{f} \ge 37$
• $3f \le 2e$
• $3\overline{f} \le 2\overline{e}$
• $f + \overline{f} \le {2 \over 3} \cdot 55 = 36 {2 \over 3}$, protislovje
• Grafa $G$ in $\overline{G}$ ne moreta biti oba ravninska.

---

Naloga 4

Naj bo $G$ regularen graf stopnje $p \ge 3$, vložen v ravnino tako, da imajo vsa lica enako število povezav $q \ge 3$ na robu. Kakšna sta lahko $p$ in $q$?

---

• $vp = 2e = fq$
• $v - e + f = 2$
• ${2e \over p} - e + {2e \over q} = 2$
• $e ({2 \over p} + {2 \over q} - 1) = 2$
• Rešitve:
  • $p = 3$: ${2 \over q} > {1 \over 3}$
    • $(p, q) = (3, 3)$, $e = 6$, $v = 4$, $f = 4$ tetraeder
    • $(p, q) = (3, 4)$, $e = 12$, $v = 8$, $f = 6$ kocka
    • $(p, q) = (3, 5)$, $e = 30$, $v = 20$, $f = 12$ dodekaeder
  • $p = 4$: ${2 \over q} > {1 \over 2}$
    • $(p, q) = (4, 3)$, $e = 12$, $v = 6$, $f = 8$ oktaeder
  • $p = 5$: ${2 \over q} > {3 \over 5}$
    • $(p, q) = (5, 3)$, $e = 30$, $v = 12$, $f = 20$ ikozaeder

---

Naloga 5

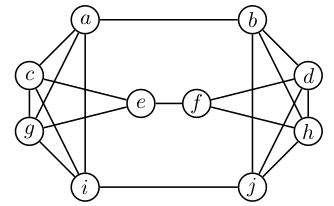
Za grafe na spodnji sliki poišči njihovo barvnost.

graph G1 {
  rankdir=LR
  node [style=filled]
  
  a [color=red]
  b [color=green]
  c [color=blue]
  d [color=blue]
  e [color=green]

  a -- b
  a -- c
  b -- c
  b -- d
  c -- e
  d -- e
}

Barvnost: 3 (imamo lih cikel, našli smo 3-barvanje)

graph G2 {
  rankdir=LR
  node [style=filled]

  a [color=red]
  b [color=green]
  c [color=green]
  d [color=green]
  h [color=green]
  e [color=red]
  f [color=red]
  g [color=red]
  k [color=red]
  i [color=green]
  j [color=green]

  d -- e
  e -- b
  e -- i
  d -- a
  b -- a
  b -- f
  i -- f
  i -- k
  d -- k
  a -- c
  f -- c
  f -- j
  k -- j
  c -- g
  j -- g
  a -- h
  k -- h
  g -- h
}

Barvnost: 2 (graf je dvodelen)

graph G3 {
  rankdir=LR
  node [style=filled]

  h -- e -- b -- a
  b -- c
  b -- d
  a -- c
  a -- d
  c -- d
  e -- f
  e -- g
  c -- f
  d -- g
  f -- g
  h -- i
  h -- j
  f -- i
  g -- j
  i -- j
  
  a [color=red]
  c [color=green]
  d [color=blue]
  b [color=magenta]
  e [color=red]
  f [color=blue]
  g [color=green]
  h [color=magenta]
  i [color=red]
  j [color=blue]
}

Barvnost je 4 (ima 4-kliko, našli smo 4-barvanje)

graph G4 {
  node [style=filled]

  a -- c
  a -- d
  b -- c
  b -- d
  a -- e
  a -- f
  b -- g
  e -- g
  f -- g
  c -- h
  g -- h
  d -- i
  g -- i
  c -- j
  e -- j
  i -- j
  d -- k
  f -- k
  h -- k
  j -- k
}

Ta stran je odprtokodna. Izboljšaj to stran.

Ta zapisek je dostopen tudi na HackMD.