Diskretne strukture (FiM)

« nazaj

Diskretne strukture (FiM) - vaje 9.12.2020

---

Urejenosti

Delna urejenost $(A, \le)$

• $x$ infimum množice $B \subseteq A$:

  \[x = \inf B \iff \forall y \in B: x \le y \land \forall z \in A: (\forall y \in B: z \le y \Rightarrow z \le x)\]

• $x$ supremum množice $B \subseteq A$:

  \[x = \sup B \iff \forall y \in B: y \le x \land \forall z \in A: (\forall y \in B: y \le z \Rightarrow x \le z)\]

---

Naloga 1

Na $\mathbb{R}^2$ definiramo relacijo $\preceq$ takole:

\[(x_1,y_1)\preceq(x_2,y_2) \Leftrightarrow x_1 \leq x_2 {\rm\;in\;} y_1 \leq y_2.\]

1. Pokaži, da je $(\mathbb{R}^2, \preceq)$ delna urejenost.
2. Določi supremum in infimum elementov $(1,3)$ in $(2,4)$ ter supremum in infimum elementov $(3,2)$ in $(4,1)$.

---

1. • refleksivnost: $(x_1, y_1) \preceq (x_1, y_1) \iff x_1 \le x_1 \land y_1 \le y_1$ velja

   • antisimetričnost:

     \[\begin{aligned} (x_1, y_1) \preceq (x_2, y_2) \land (x_2, y_2) \preceq (x_1, y_1) &\Rightarrow x_1 \le x_2 \land y_1 \le y_2 \land x_2 \le x_1 \land y_2 \le y_1 \\ &\Rightarrow x_1 = x_2 \land y_1 = y_2 \\ &\Rightarrow (x_1, y_1) = (x_2, y_2) \end{aligned}\]

   • tranzitivnost:

     \[\begin{aligned} (x_1, y_1) \preceq (x_2, y_2) \land (x_2, y_2) \preceq (x_3, y_3) &\Rightarrow x_1 \le x_2 \land y_1 \le y_2 \land x_2 \le x_3 \land y_2 \le y_3 \\ &\Rightarrow x_1 \le x_3 \land y_1 \le y_3 \\ &\Rightarrow (x_1, y_1) \preceq (x_3, y_3) \end{aligned}\]
2. • $\sup\lbrace (1, 3), (2, 4) \rbrace = (2, 4)$
   • $\inf\lbrace (1, 3), (2, 4) \rbrace = (1, 3)$
   • $\sup\lbrace (3, 2), (4, 1) \rbrace = (4, 2)$
   • $\inf\lbrace (3, 2), (4, 1) \rbrace = (3, 1)$
   • $\sup\lbrace (x_1, y_1), (x_2, y_2) \rbrace = (\max\lbrace x_1, x_2 \rbrace, \max\lbrace y_1, y_2 \rbrace)$
   • $\inf\lbrace (x_1, y_1), (x_2, y_2) \rbrace = (\min\lbrace x_1, x_2 \rbrace, \min\lbrace y_1, y_2 \rbrace)$

---

Teorija grafov

(Neusmerjen) graf $G = (V, E)$

• $V$ je množica vozlišč
• $E \subseteq {V \choose 2} = \lbrace \lbrace u, v \rbrace \mid u, v \in V, u \ne v \rbrace$ je množica povezav

graph G {
  a -- b
  a -- c
  b -- d
  c -- e
  d -- e
  c -- f
  b -- f
  f -- g
  d -- g
  e -- g
}

• Stopnja vozlišča $u \in V$: $d_G(u) = d(u) = |\lbrace e \in E \mid u \in e \rbrace|$
• Maksimalna stopnja grafa $\Delta(G) = \max_{u \in V} d_G(u)$
• Minimalna stopnja grafa $\delta(G) = \min_{u \in V} d_G(u)$
• Graf je dvodelen, če lahko zapišemo $V = A + B$, tako da za vsako povezavo $\lbrace u, v \rbrace \in E$ velja $u \in A$, $v \in B$

• Grafa $G_1 = (V_1, E_1)$ in $G_2 = (V_2, E_2)$ sta izomorfna, če obstaja bijektivna preslikava $f : V_1 \to V_2$, tako da velja

  \[\forall u, v \in V_1: (\{u, v\} \in E_1 \iff \{f(u), f(v)\} \in E_2)\]

---

Naloga 2

Dan je graf $G=(V,E)$, kjer je $V = \lbrace 1,2,3,4,5 \rbrace$ in $E = \lbrace \lbrace 1,2 \rbrace, \lbrace 1,4 \rbrace, \lbrace 1,5 \rbrace, \lbrace 2,3 \rbrace, \lbrace 2,4 \rbrace, \lbrace 3,4 \rbrace, \lbrace 4,5 \rbrace \rbrace$.

1. Čim lepše nariši graf $G$.
2. Poišči stopnje vseh vozlišč ter minimalno in maksimalno stopnjo grafa $G$. Ali je graf regularen?
3. Ali je graf dvodelen?

---

1. graph G {
   1 -- 2
   1 -- 4
   1 -- 5
   2 -- 3
   2 -- 4
   3 -- 4
   4 -- 5
   }
   

2. • $\delta(G) = 2$
   • $\Delta(G) = 4$
   • zaporedje stopenj: $2, 2, 3, 3, 4$
   • graf ni regularen
3. Graf ni dvodelen, saj vsebuje lihe cikle (trikotniki, petkotnik).

---

Naloga 3

Na zabavi se je zbralo $13$ ljudi. Vsak je s seboj prinesel $3$ darila, ki bi jih rad izmenjal s tremi drugimi udeleženci zabave. Ali je to izvedljivo? Predstavi kot problem iz teorije grafov in ga reši.

---

• $G = (V, E)$
• $V$ … udeleženci zabave, $|V| = 13$
• $\lbrace u, v \rbrace \in E$ … $u$ in $v$ si izmenjata darilo
• $d_G(u) = 3$ za vse $u \in V$

Lema o rokovanju: $\sum_{u \in V} d_G(u) = 2 |E|$

• $39 = \sum_{u \in V} d_G(u) = 2 |E|$
• $|E| = 19.5$ protislovje

To torej ni izvedljivo.

---

Naloga 4

Ali sta spodnja grafa izomorfna?

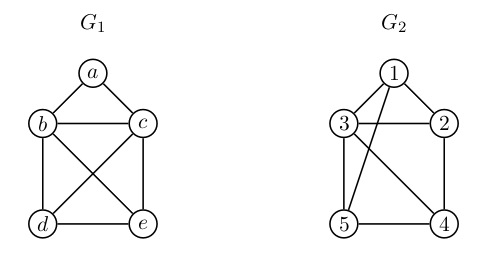
• $|V_1| = |V_2| = 5$
• $|E_1| = |E_2| = 8$
• stopnje vozlišč - zaporedje stopenj:
  • $G_1$: 2, 3, 3, 4, 4
  • $G_2$: 3, 3, 3, 3, 4
  • grafa nista izomorfna

---

Naloga 5

Ali sta spodnja grafa izomorfna?

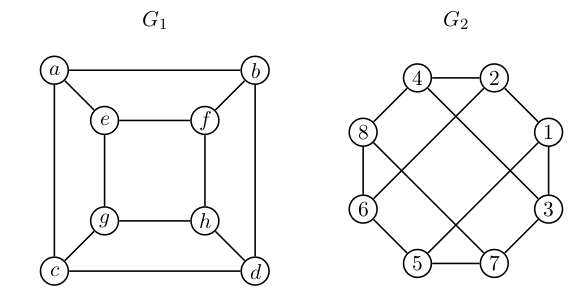
• $|V_1| = |V_2| = 8$
• $|E_1| = |E_2| = 12$
• oba grafa sta $3$-regularna
• izomorfizem:
  • $a \to 1$
  • $b \to 2$
  • $c \to 3$
  • $e \to 5$
  • $f \to 6$
  • $g \to 7$
  • $d \to 4$
  • $h \to 8$
• grafa sta izomorfna

---

Naloga 6

Ali sta spodnja grafa izomorfna? Nasvet: v vsakem od grafov preštej cikle dolžine $4$.

---

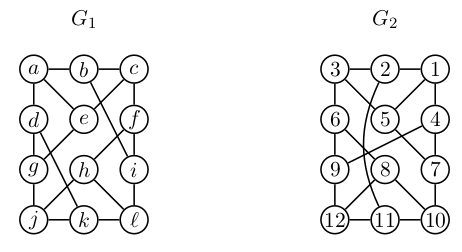
• $|V_1| = |V_2| = 12$
• oba grafa sta $3$-regularna
• cikli dolžine $4$:
  • $G_1$: 6 ciklov dolžine 4
    • abce
    • adge
    • bcfi
    • dgjk
    • fhli
    • hjkl
  • $G_2$: 4 cikli dolžine 4
    • 1, 2, 3, 5
    • 1, 4, 7, 5
    • 6, 8, 12, 9
    • 8, 10, 11, 12
  • grafa nista izomorfna

Ta stran je odprtokodna. Izboljšaj to stran.

Ta zapisek je dostopen tudi na HackMD.