Computational Geometry
Computational geometry - Tutorial 26.5.2021
Range trees
class AssociatedTree:
def __init__(self, ordered, dim, dims):
points = ordered[dim]
n = len(points)
h = (n-1) // 2
self.split = points[h][dim]
self.dim = dim
self.left = self.right = self.assoc = self.point = None
self.next = self.first = self.last = None
if n > 1:
left = [[p for p in pts if p[dim] <= self.split] for pts in ordered]
right = [[p for p in pts if p[dim] > self.split] for pts in ordered]
self.left = AssociatedTree(left, dim, dims)
self.first = self.left.first
self.right = AssociatedTree(right, dim, dims)
self.last = self.right.last
self.left.last.next = self.right.first
else:
self.point, = points
self.first = self.last = self
if dim < dims - 1:
self.assoc = AssociatedTree(ordered, dim+1, dims)
def query(self, left, right):
if self.point is not None:
if left[self.dim] <= self.split <= right[self.dim]:
yield from self.report(left, right)
return
elif right[self.dim] <= self.split:
yield from self.left.query(left, right)
elif left[self.dim] > self.split:
yield from self.right.query(left, right)
else:
yield from self.left.left_descent(left, right)
yield from self.right.right_descent(left, right)
def left_descent(self, left, right):
if self.point is not None:
if left[self.dim] <= self.split:
yield from self.report(left, right)
return
if left[self.dim] > self.split:
yield from self.right.left_descent(left, right)
else:
yield from self.left.left_descent(left, right)
yield from self.right.report(left, right)
def right_descent(self, left, right):
if self.point is not None:
if right[self.dim] >= self.split:
yield from self.report(left, right)
return
if right[self.dim] <= self.split:
yield from self.left.right_descent(left, right)
else:
yield from self.left.report(left, right)
yield from self.right.right_descent(left, right)
def report(self, left, right):
if self.assoc is not None:
yield from self.assoc.query(left, right)
else:
p = self.first
while p != self.last:
yield p.point
p = p.next
yield p.point
class RangeTree:
def __init__(self, points, dims):
assert len(points) > 0
ordered = [sorted(points, key=lambda p, i=i: p[i]) for i in range(dims)]
self.tree = AssociatedTree(ordered, 0, dims)
def query(self, left, right):
yield from self.tree.query(left, right)
- Space complexity: $O(n \log^{d-1} n)$
- Construction: $O(n \log^{d-1} n)$
- Query: $O(\log^d n + k)$, where $k$ is the number of reported points
Exercise 1
We are given a set $P$ of $n$ points in a plane. We want to design a dynamic data structure which stores a subset $Q \subseteq P$. At the beginning, we have $Q = P$. The data structure should be able to perform the following operations in $O(\log^2 n)$ time:
- Deleting a point $p \in Q$ from $Q$.
- Inserting a point $p \in P \setminus Q$ into $Q$,
- Counting $\vert Q \cap R \vert$ for a query rectangle $R$.
- At each node $u$ of the last level tree, store the number of points in $Q$ in the leaves of the subtree rooted in $u$.
- Deleting $p$:
- Find $p$ in the main tree, and ascend to the root and fix every associated tree of the nodes in the path
- Fixing: find $p$ in the associated tree, and ascend to its root, decreasing counts at each nod in the path
- Inserting $p$:
- Find $p$ in the main tree, and ascend to the root and fix every associated tree of the nodes in the path
- Fixing: find $p$ in the associated tree, and ascend to its root, increasing counts at each nod in the path
- Counting query:
- Similar to a normal query, but instead of reporting points we return the stored counts and sum them up
Exercise 2
We are given a set $P$ of $n$ points in $\mathbb{R}^d$, where $d$ is constant. We want to design a data structure which stores $P$ and allows partial queries. A partial query is given by values for a subset of coordinates, and its result is the set of points which match the given coordinates.
- Explain how to perform partial queries in $\mathbb{R}^2$ with a $2$-dimensional range tree. What is the time complexity of the query?
- Describe a data structure with linear space complexity which can perform partial queries in $O(\log n + k)$ time. Keep in mind that we may use $O(d 2^d n)$ space, where $d$ is constant.
Example partial queries in $\mathbb{R}^3$:
- find all points with $x = 1, y = 2$
- find all points with $y = 2, z = -1$
- find all points with $y = 2$
- find all points with $x = 1, y = 2, z = 3$
-
inf = float('inf') def partial_query(tree, x=None, y=None): if x is None: xmin = -inf xmax = inf else: xmin = xmax = x if y is None: ymin = -inf ymax = inf else: ymin = ymax = y yield from tree.query(left=[xmin, ymin], right=[xmax, ymax])- Time complexity: $O(\log^2 n + k)$
- Space complexity: $O(n \log n)$
-
Suppose we are given points $({x_1^{(i)}}, {x_2^{(i)}}, \dots, {x_d^{(i)}})$ ($1 \le i \le n$).
- For every $I \subseteq \lbrace 1, 2, \dots, d \rbrace$, make an array by sorting lexicographically by $({x_j})_{j \in I}$
- For a partial query giving values for coordinates of the dimensions in $I \subseteq \lbrace 1, 2, \dots, d \rbrace$, perform a bisection and then walk left and right to report all the points
Exercise 3
Let $H$ be a set of at most $n$ horizontal segments and let $V$ be a set of at most $n$ vertical segments. We want to find an algorithm which determines the number of intersecting pairs from $H \times V$ in $O(n \log n)$ time.
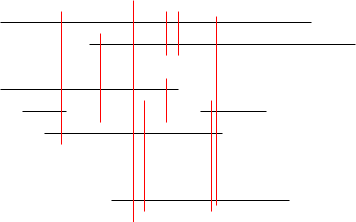
- Let $P$ be a set of $n$ points in $\mathbb{R}$. Describe a dynamic data structure which stores a subset $Q\subseteq P$ and can perform the following operations in $O(\log n)$ time: adding an element of $P \setminus Q$, deleting an element from $Q$, and counting points $Q \cap I$ for a given interval $I$.
- Describe an algorithm which determines the number of intersecting pairs from $H \times V$ in $O(n \log n)$ time.
- Use the associated tree structure from Exercise 1.