Computational Geometry
Computational geometry - Tutorial 12.5.2021
Voronoi diagrams
Voronoi diagram of a set $P$ of points in a plane (sites): subdivision of the plane into cells according to the closest point of $P$
Exercise 1
Construct the Voronoi diagram of the points $(0, 0), (3, 2), (1, 5), (4, 4), (5, 8), (6, 1)$.
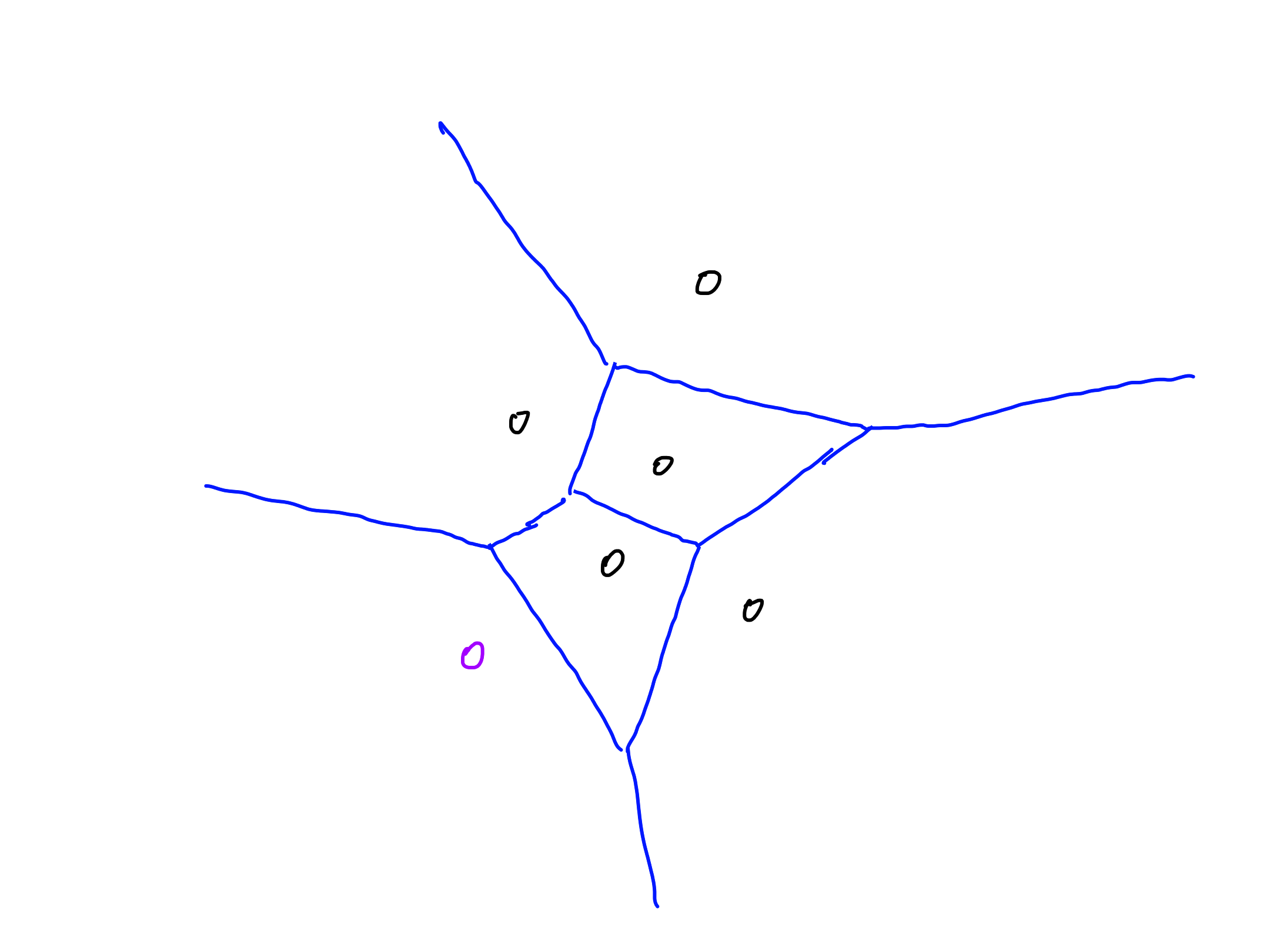
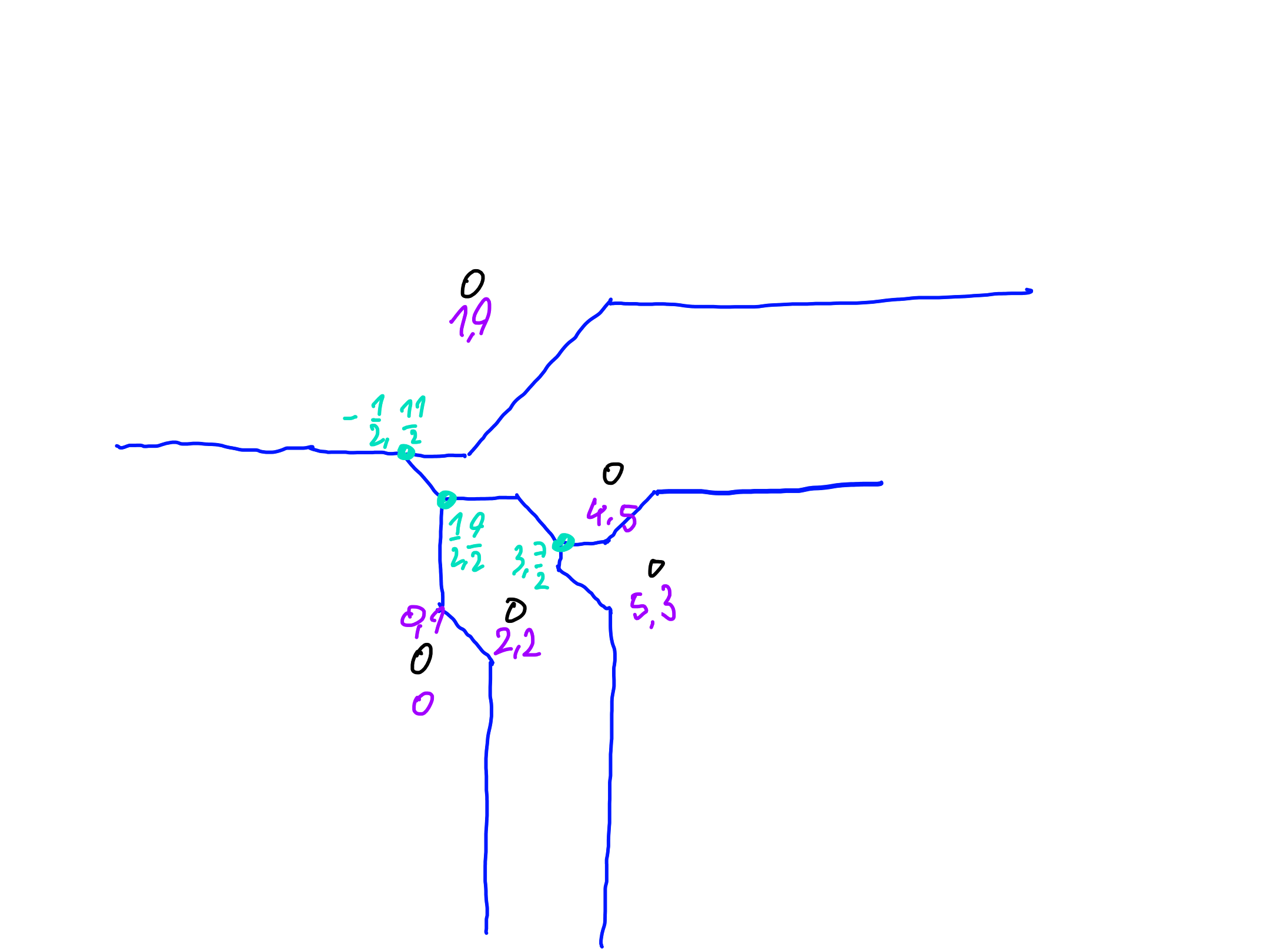
Exercise 2
Construct the Voronoi diagram of the points $(0, 1), (2, 2), (4, 5), (6, 3), (1, 9)$ for the ${L_1}$-distance. Write down the coordinates of Voronoi vertices.
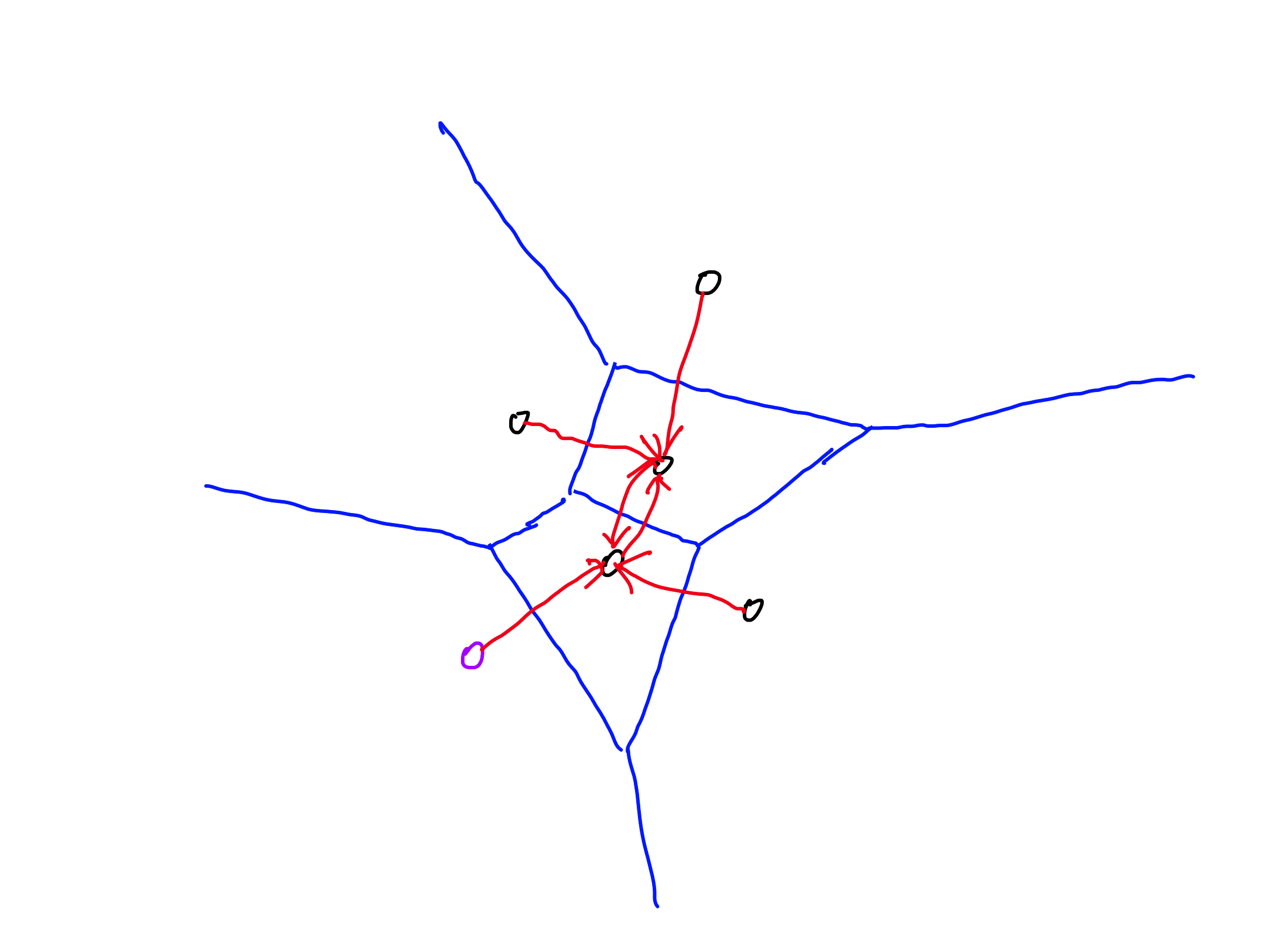
Exercise 3
Let $P$ be a set of $n$ points in a plane. For each point $p \in P$, we want to find the closest point ${q_p} \in P$ - i.e., such that $\vert p {q_p} \vert = \min \lbrace \vert pq \vert \mid q \in P \setminus \lbrace p \rbrace \rbrace$. Describe an algorithm which finds the point ${q_p}$ for every point $p \in P$ in $O(n \log n)$ time.
- Construct the Voronoi diagram of $P$ ($O(n \log n)$)
- For each point $p \in P$, consider the sites corresponding to the neighboring cells to the cell corresponding to $p$ and determine ${q_p}$ to be the closest point to $p$ among them ($O(n)$)
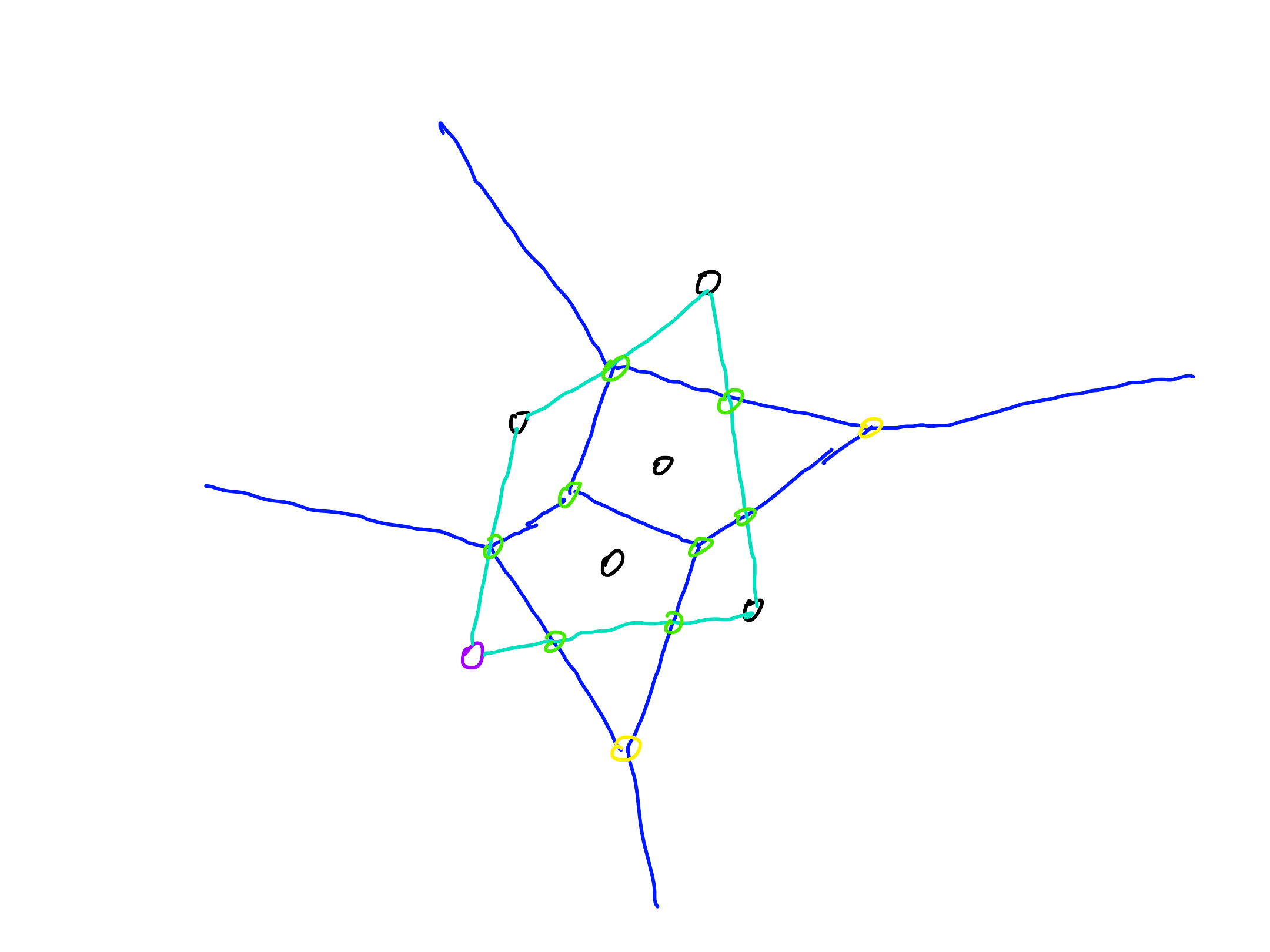
Exercise 4
Let $P$ be a set of points in a plane. Describe an algorithm which finds the largest disk $D$ with its center in $\operatorname{CH}(P)$ which does not contain any point of $P$.
- Construct the Voronoi diagram of $P$ ($O(n \log n)$)
- For each Voronoi vertex $v$, check for intersection of any infinite ray with the segment $s$ between the corresponding sites
- If any infinite ray has no such intersection, $v$ is outside $\operatorname{CH}(P)$ and we consider the intersections of the other edges with endpoint $v$ with $s$
- Otherwise, consider the point $v$
- Among the considered point, find one with maximal distance to the neighboring sites
Exercise 5
Let $B$ and $R$ be sets of $n$ blue and red points in a plane, respectively. Describe an algorithm which computes
\[\min\{d(b, r) \mid b \in B, r \in R\}\]in $O(n \log n)$ time, where $d(\cdot, \cdot)$ is the Euclidean distance.
- Construct the Voronoi diagram of $R$ ($O(n \log n)$)
- Construct a point location data structure on the Voronoi diagram (expected $O(n \log n)$)
- For each $b \in B$, find the Voronoi cell containing $b$ and assign it the site $r_b$ (expected $O(n \log n)$)
- Return $\min{d(b, r_b) \mid b \in B}$ ($O(n)$)
Exercise 6
Let $P$ be a set of $n$ points in a plane representing “obstacles”. Let $D(x)$ be a disk of radius $1$ with its center in the point $x \in \mathbb{R}^2$. Let $s, t \in \mathbb{R}^2$ be two distinct points such that $P \cap D(s) = P \cap D(t) = \emptyset$. Describe an $O(n \log n)$ time algorithm which decides whether there is a continuous curve $x(r)$ such that $x(0) = s$ and $x(1) = t$ and $D(x(r)) \cup P = \emptyset$ for all $r \in [0, 1]$. Less formally, we are interested in whether a disk of diameter $1$ can be moved continuously from the position with center $s$ to the position with center $t$ without touching the points of $P$.
Exercise 7
Let $P$ be a set of $n$ points in a plane. We are interested in the maximal distances Voronoi diagram. For each point $p\in P$, let
\[\operatorname{cell}(p) = \{ x \in \mathbb{R}^2 \mid d(p, x) \ge d(q, x) \text{ for each } q \in P \setminus \{p\} \}.\]- Is $\operatorname{cell}(p)$ a convex set? What if we are in $\mathbb{R}^d$?
- Prove that $\operatorname{cell}(p) \ne \emptyset$ if and only if $p$ is an extremal point in $\operatorname{CH}(P)$.
- Let $E$ be the edge set of the diagram, i.e., the set of the points in the plane contained in $\operatorname{cell}(p) \cap \operatorname{cell}(p’)$ for some $p \ne p’$. Show that $E$ does not contain a closed curve - i.e., structurally, $E$ is a tree.
- Prove the lower bound $\Omega(n \log n)$ for the computation of the maximal distances Voronoi diagram.
- Describe na algorithm which computes the maximal distances Voronoi diagram in $O(n \log n)$ time.