Computational Geometry
Computational geometry - Tutorial 5.5.2021
Duality
- $(O, x, y) \to (Q, u, v)$
- $p({p_x}, {p_y}) \to p^*: v = {p_x} u - {p_y}$
- $\ell: y = kx + n \to \ell^*(k, -n)$
Exercise 1
Let $P$ be a set of $n$ points in a plane. A point $x \in \mathbb{R}^2$, not necessarily from $P$, is a central point for $P$ if the following holds: every half-plane containing $x$ contains at least $n/3$ points of $P$.
- What does this mean in the dual space?
- Describe an algorithm which finds a central point if it exists.
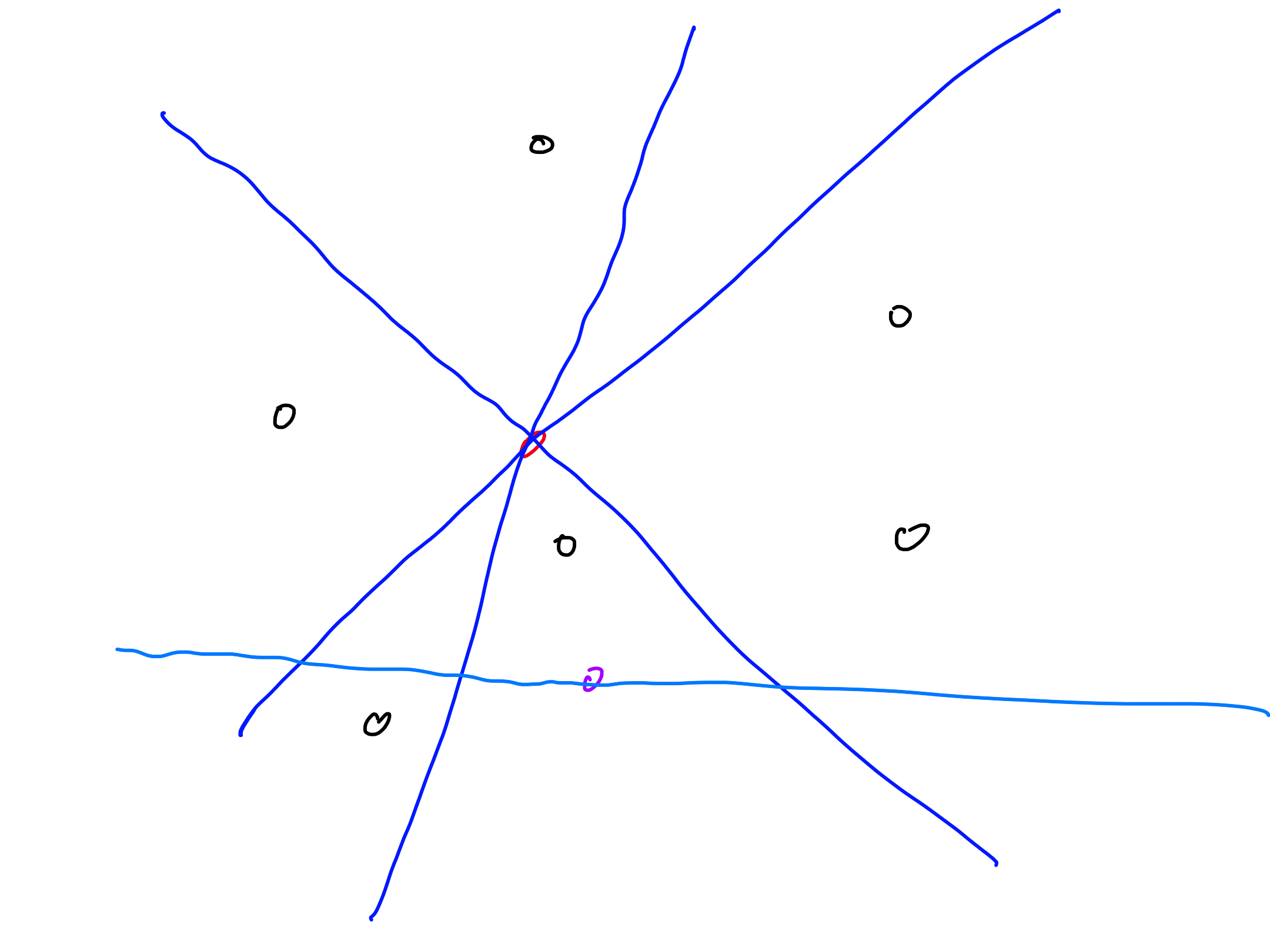
Algorithm:
- determine the lines dual to the points of $P$ ($O(n)$)
- perform a sweep-line algorithm to determine the paths bounding the upper and lower $n/3$ of the lines ($O(n^2 \log n)$)
- compute the lower hull of the upper path and the upper hull of the lower path ($O(n)$)
- if the hulls do not intersect, then we can draw a line $x^*$ between them which is dual to a central point $x$ ($O(n)$)
- if the hulls intersect, then there is no central point

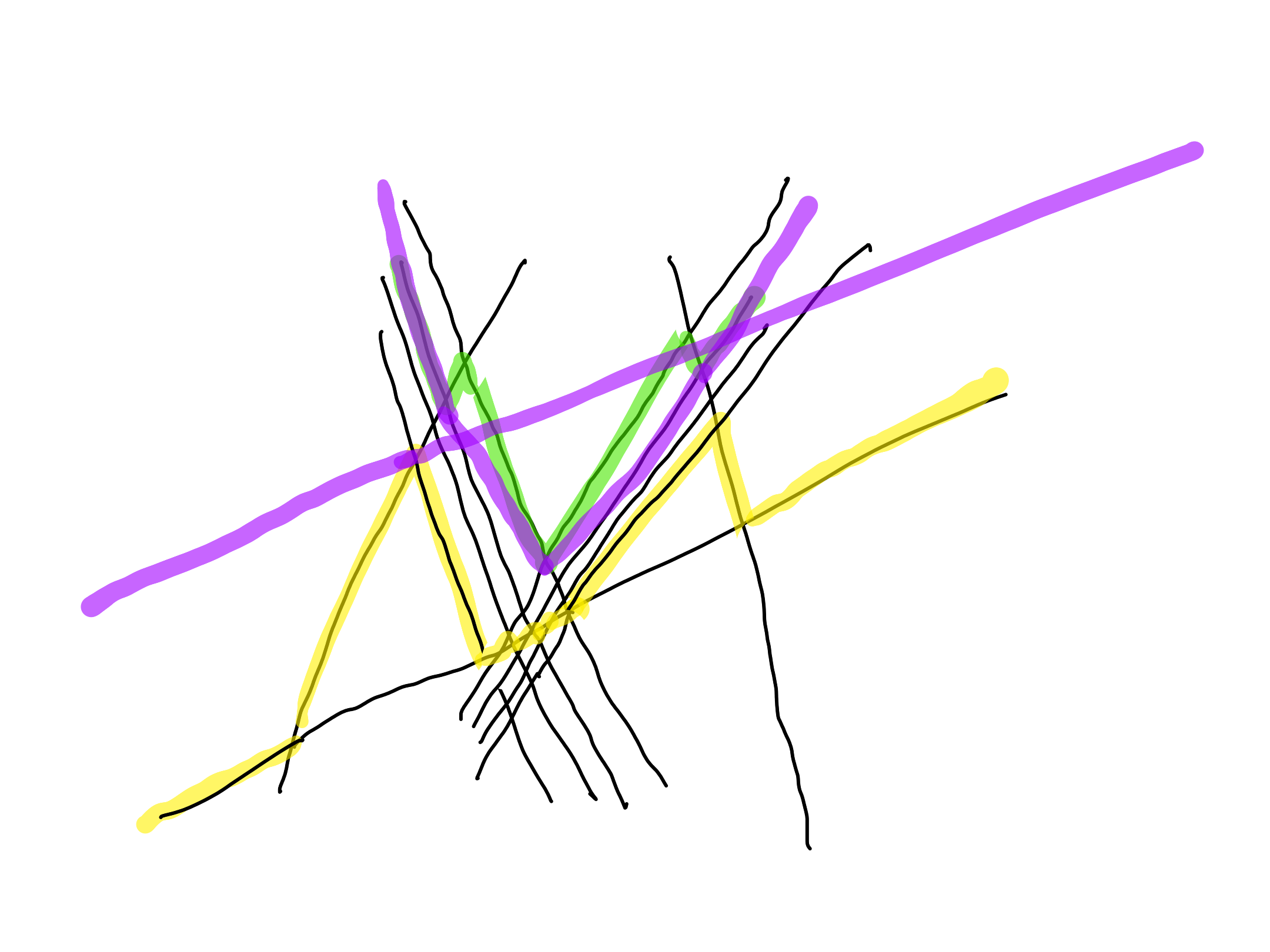
Exercise 2
Let $S$ be a set of $n$ segments in a plane.
- Describe an algorithm which decides in $O(n^2)$ time whether there exists a line intersecting every segment of $S$.
- Describe an algorithm which returns a line intersecting the largest number of segments of $S$.

Algorithm:
- determine the dual wedges of the segments
- perform a sweep-line algorithm maintaining the order of the lines bounding the wedges and the number of wedges each interval between the lines belongs to
- if we find an interval contained in $n$ wedges, then a point in it is the dual of a line intersecting all segments of $S$
- we can remember the interval contained in the largest number of wedges to determine the line intersecting the largest number of segments
Time complexity: $O(n^2 \log n)$
