Computational Geometry

« nazaj

Computational geometry - Tutorial 28.4.2021

---

DCEL

DCEL: doubly connected edge list

• vertex $v$
  • edge: an incident semi-edge originating in $v$
  • coordinates
• semi-edge $e$:
  • origin: the origin vertex
  • twin: the opposite semi-edge corresponding to the same edge
  • next: the next semi-edge on the same face
  • prev: the previous semi-edge on the same face
  • face: the incident face
• face $f$:
  • outer_component: an incident semi-edge from the outer boundary of $f$
  • inner_components: a list containing one incident semi-edge for each inner boundary of $f$

---

Exercise 1

We are given a DCEL of a connected subdivision in a plane. Each face of the subdivision, except for the outer face, is convex. Give an efficient pseudocode for the following tasks.

1. Given a face $f$, list the vertices of $f$.
2. Given a face $f$, determine whether $f$ is the outer face.
3. Given a vertex $v$, find the faces incident to $v$.
4. Given a vertex $v$, find the vertex of the DCEL with the smallest $x$-coordinate.
5. Given a face $f$, list the faces with at least one vertex in common with $f$.
6. Given a line $\overline{pq}$ intersecting the edges of the DCEL (but not its vertices) and a face $f$ containing $p$, update the DCEL to represent a new subdivision which includes $\overline{pq}$.

---

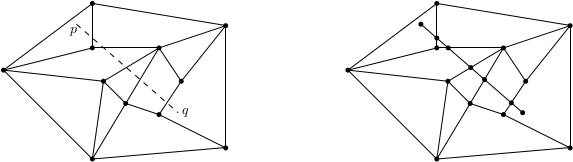
1. def vertices(f):
       if f.outer_component is None:
           e0 = f.inner_components[0]
       else:
           e0 = f.outer_component
       vcs = [e0.origin]
       e = e0
       while e.next != e0:
           e = e.next
           vcs.append(e.origin)
       return vcs
   

2. def outer_face(f):
       return f.outer_component is None
   

3. def faces(v):
       e0 = v.edge
       fcs = [e0.face]
       e = e0
       while e.twin.next != e0:
           e = e.twin.next
           fcs.append(e.face)
       return fcs
   

4. • let $f$ be a face incident to $v$ (f = v.edge.face)
   • if $f$ is the outer face, return its leftmost vertex
   • find the semi-edge $e$ originating in the leftmost vertex of $f$
   • set f = e.twin.face and repeat

5. def common_vertex(f):
       if f.outer_component is None:
           e0 = f.inner_components[0]
       else:
           e0 = f.outer_component
       fcs = set()
       e = e0
       fcs.union(faces(e.origin))
       while e.next != e0:
           e = e.next
           fcs.union(faces(e.origin))
       fcs.remove(f)
       return fcs
   

6. def add_segment(f, p, q):
       find semi-edge e incident to f such that pq intersects e in a point v
       p.edge = Edge()
       v.edge = Edge()
       v.edge.origin = v
       v.edge.face = f
       v.edge.next = e.next
       v.edge.prev = p.edge
       v.edge.twin = e.twin
       e.next.prev = v.edge
       e.next = Edge()
       e.twin.twin = v.edge
       e.twin = Edge()
       e.twin.origin = v
       e.twin.face = v.edge.twin.face
       e.twin.next = v.edge.twin.next
       e.twin.prev = v.edge.twin
       e.twin.twin = e
       e.twin.next.prev = e.twin
       e.twin.prev.next = e.twin
       e.next.origin = v
       e.next.face = f
       e.next.next = v.edge.prev
       e.next.prev = e
       e.next.twin = v.edge.prev
       p.edge.origin = p
       p.edge.face = f
       p.edge.next = v.edge
       p.edge.prev = e.next
       p.edge.twin = e.next
       f = e.twin.face
       while pq has another intersection u with the boundary of f:
           split the face f with uv
           f = face on the other side of the edge split by u
           v = u
       add the segment vq
   

---

Exercise 2

We are given a DCEL representing a subdivision of the plane and a face $f$ of this subdivision. Assume that each face of the subdivision is defined by a cycle of edges without repetitions. We want to delete all edges incident to $f$, i.e., we delete the edges from the set $D = \lbrace e \mid e \text{ is an edge of } f \rbrace$. Assume that the subdivision remains connected after $D$ is deleted. Write the pseudocode for deleting the edges of $D$ and updates the DCEL. What is the time complexity of the algorithm?

---

Arrangements

Exercise 3

Let $H$ be a set of $n$ lines in the plane which intersect in the same point $p$, and let $H’$ be a set of $m$ lines in the plane which intersect in another point $p’ \ne p$. The lines of $H$ do not contain $p’$ and the lines of $H’$ do not contain $p$.

1. How many vertices, edges and faces does the arrangement $\mathcal{A}(H)$ have?
2. How many vertices, edges and faces does the arrangement $\mathcal{A}(H \cup H’)$ have?
3. Let $R$ be a set of $n$ planes in $\mathbb{R}^3$. Each plane of $R$ contains the point $(0, 0, 0)$, and no triple of planes intersects in a line. How many vertices, edges, faces and cells does the arrangement $\mathcal{A}(R)$ have?

---

$v - e + f = 1$ (since we have a connected arrangement with infinite edges)

1. $v = 1$, $e = 2n$, $f = 2n$

---

Exercise 4

Let ${L_h}$ and ${L_v}$ be sets of $n$ horizontal lines and $n$ vertical lines in a plane, respectively. Let ${L_p}$ be a set of $n$ lines in a plane intersecting in a point $p$. No line of ${L_p}$ is horizontal or vertical and no line from ${L_h}$ or ${L_v}$ contains the point $p$. Furthermore, no three lines ${\ell_h} \in {L_h}, {\ell_v} \in {L_v}, {\ell_p} \in {L_p}$ intersect in the same point.

1. How many vertices, edges and faces does the arrangement $\mathcal{A}({L_h} \cup {L_v} \cup L_p)$ have?
2. Describe the points dual to ${L_h} \cup {L_p}$.

Ta stran je odprtokodna. Izboljšaj to stran.

Ta zapisek je dostopen tudi na HackMD.