Computational Geometry

« nazaj

Computational geometry - Tutorial 21.4.2021

---

Convexity

Exercise 1

Describe a data structure for storing a convex polygon $P$ which allows us to find out in $O(\log n)$ time whether a query point is contained in $P$. The data structure should be constructed in linear time.

---

Data structure:

• the structure itself
• construction algorithm
• query algorithm

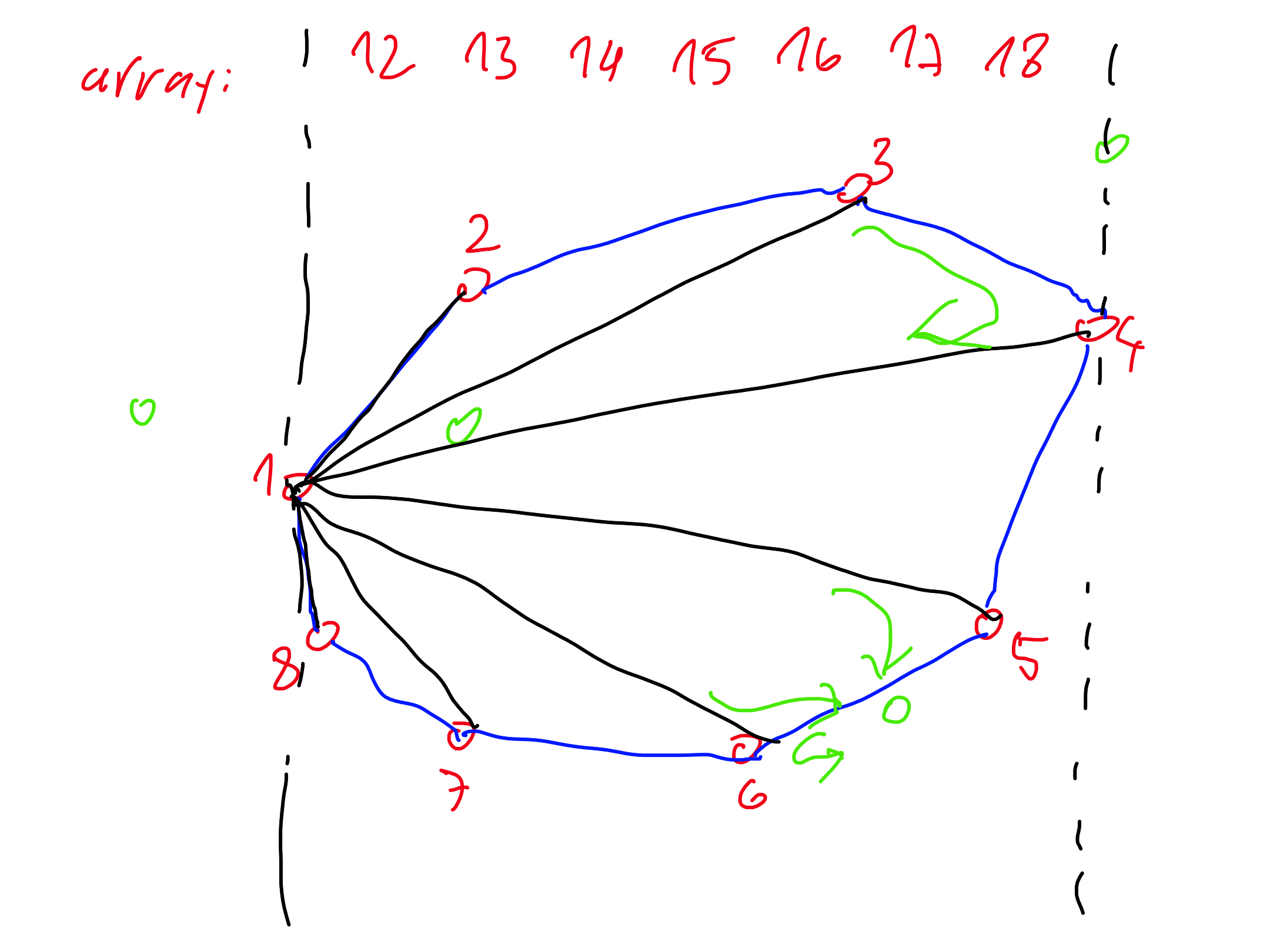
Structure: array

Construction:

• pick a vertex $u$ and add segments $uv$ to each vertex $v \ne u$ in order to the array ($O(n)$ time)

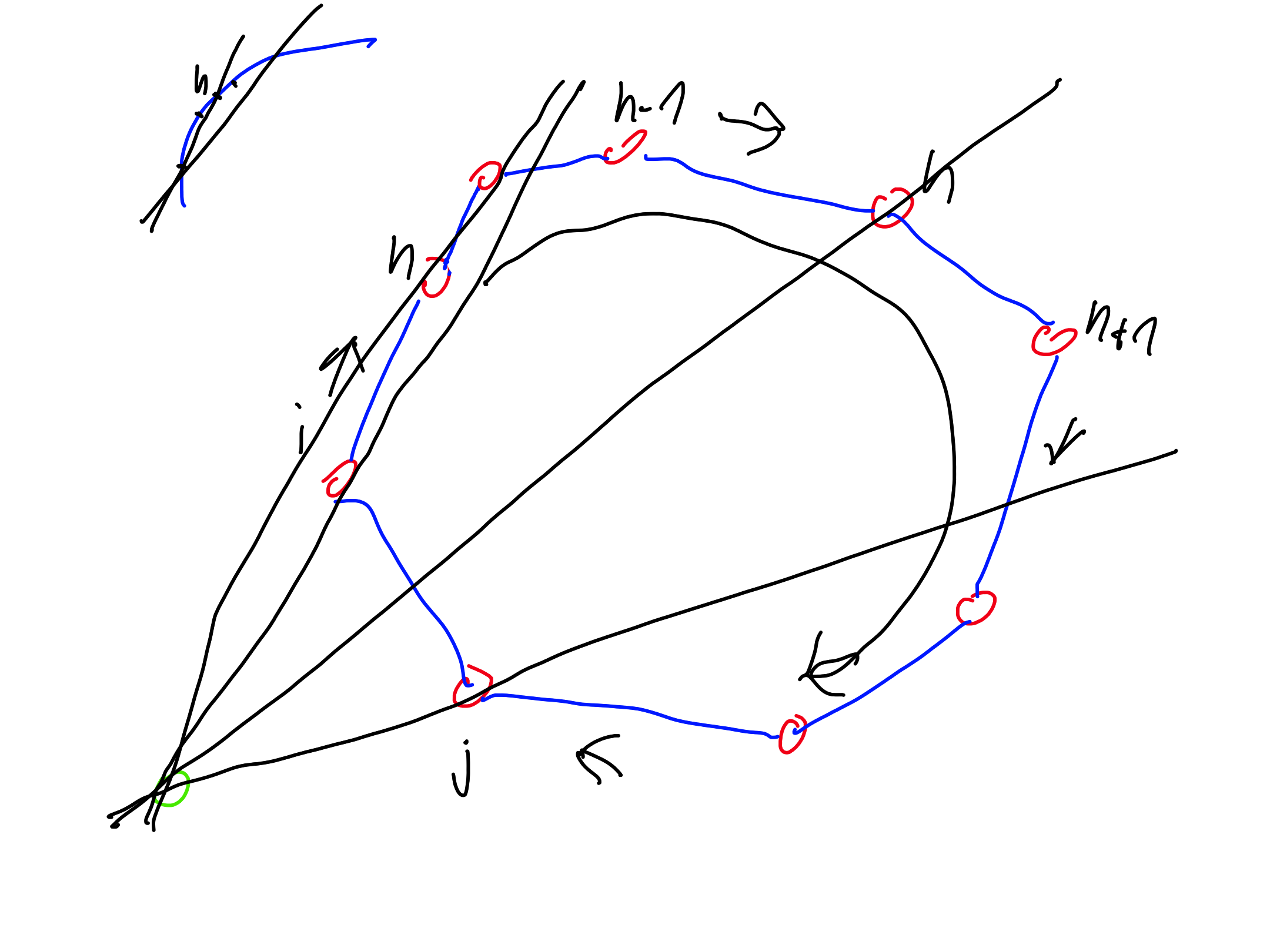
Query for a point $p$ (assume clockwise orientation):

• perform a bisection to determine two neighboring segments $uv, uw$ in the array such that $p$ lies between them (i.e., $uvp$ is a right turn and $uwp$ is a left turn) ($O(\log n)$ time)
• if $p$ is before the first or after the last segment, then we return False
• otherwise, if $vwp$ is a right turn, return True, if it is a left turn, return False

---

Exercise 2

We are given two convex polygons $P, Q$. Describe a linear time algorithm which computes $\operatorname{CH}(P \cup Q)$. You may assume that $P$ and $Q$ are disjoint.

---

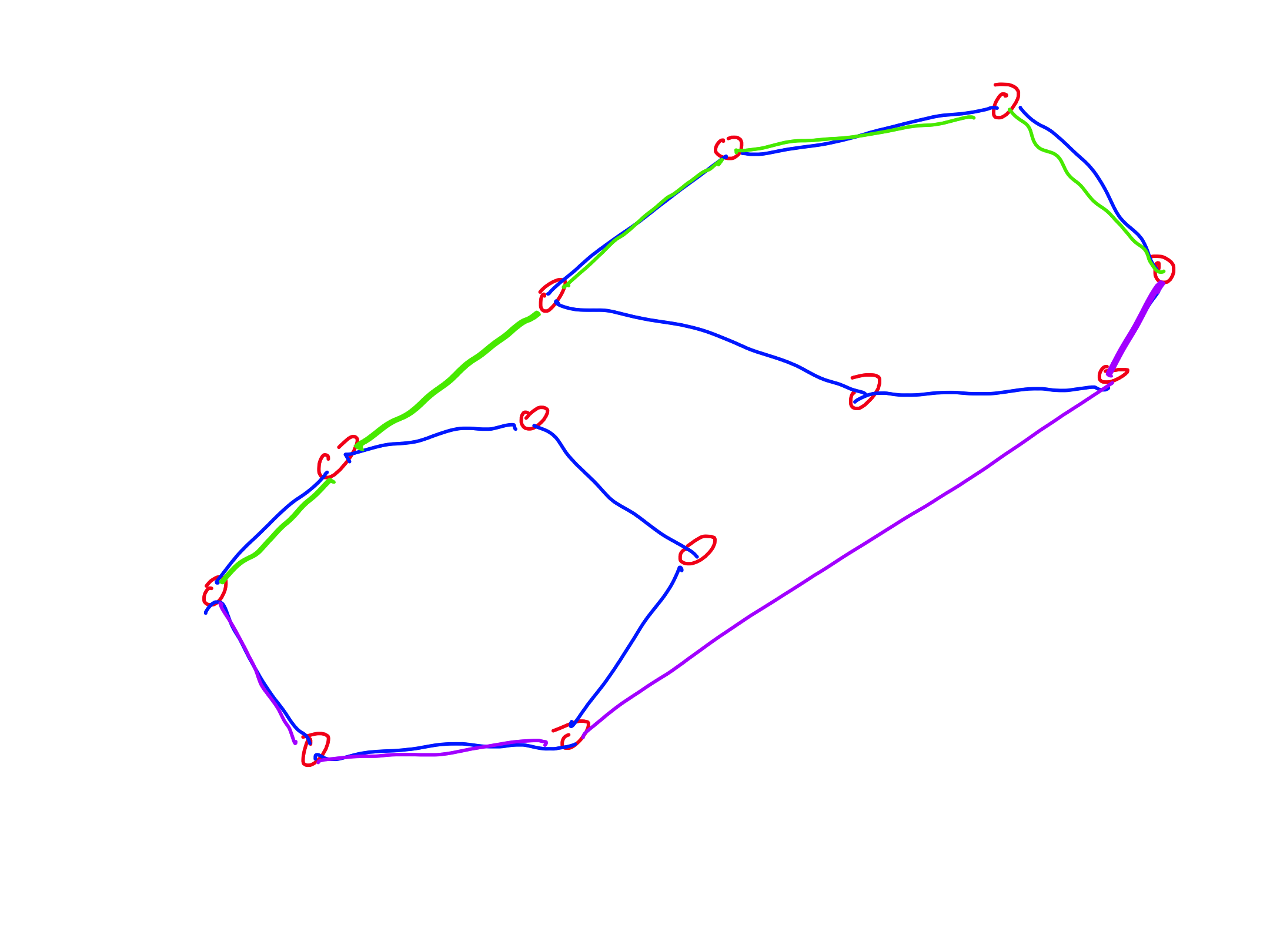
• determine the upper and lower paths of $P$ and $Q$ ($O(n)$)
• merge the two upper paths and the two lower paths ($O(n)$)
• perform the incremental algorithm on the two paths ($O(n)$)

This also works if the polygons are not disjoint!

---

Exercise 3

We are given a convex polygon $P$ as an array of vertices $p[1, \dots ,n]$.

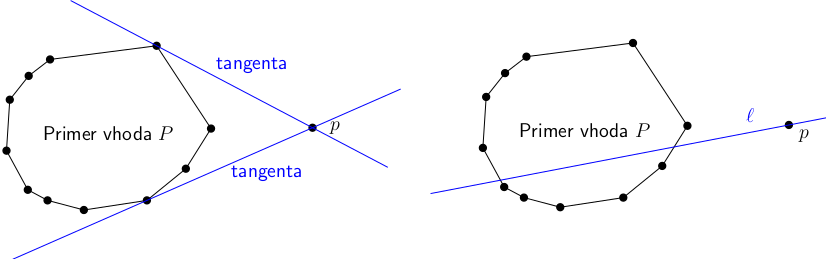
1. Describe an $O(\log n)$ algorithm which finds the highest vertex of $P$.
2. Describe an $O(\log n)$ algorithm which finds both tangents of the polygon $P$ through a given point $p \in \mathbb{R}^2 \setminus P$.
3. Describe an $O(\log n)$ algorithm which finds the intersection of $P$ and a given line $\ell$.
4. Describe an $O(\log n)$ algorithm which finds the point of $P$ which is closest to the given line $\ell$.

---

1. def highestPoint(p):
       n = len(p)
          
       def rising(i):
           return p[(i+1) % n].y > p[i].y
          
       i, j = 0, n-1
       if rising(j) and not rising(i):
           return p[i]
       while j - i > 1:
           h = (i+j) // 2
           if rising(i):
               if not rising(h) or p[h].y < p[i].y:
                   j = h
               else:
                   i = h
           else:
               if rising(h) or p[h].y < p[i].y:
                   i = h
               else:
                   j = h
       if p[i].y > p[j].y:
           return p[i]
       else:
           return p[j]
   

2. Do the bisection:
   • If both neighboring vertices lie on the same side of the line, then the line is a tangent.
   • Otherwise, move according to whether the previous or the next point lies above the line.
   • Do this for each tangent separately.

Ta stran je odprtokodna. Izboljšaj to stran.

Ta zapisek je dostopen tudi na HackMD.