Computational Geometry
Computational geometry - Tutorial 14.4.2021
Convexity
Exercise 1
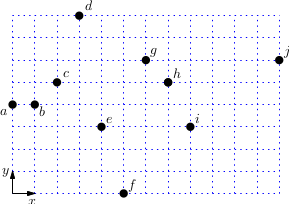
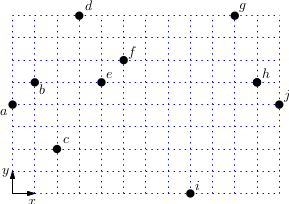
We are given a set of $10$ points ${\mathcal P} = \lbrace a, b, \dots, j \rbrace$. For the incremental algorithm and Graham’s algorithm, specify the triples of points $(X, Y, Z) \in {\mathcal P}^3$ for which the algorithms checks whether the sequence $X,Y,Z$ is a right turn. The triples should be listed in the same order in which the algorithm considers them.


Exercise 2
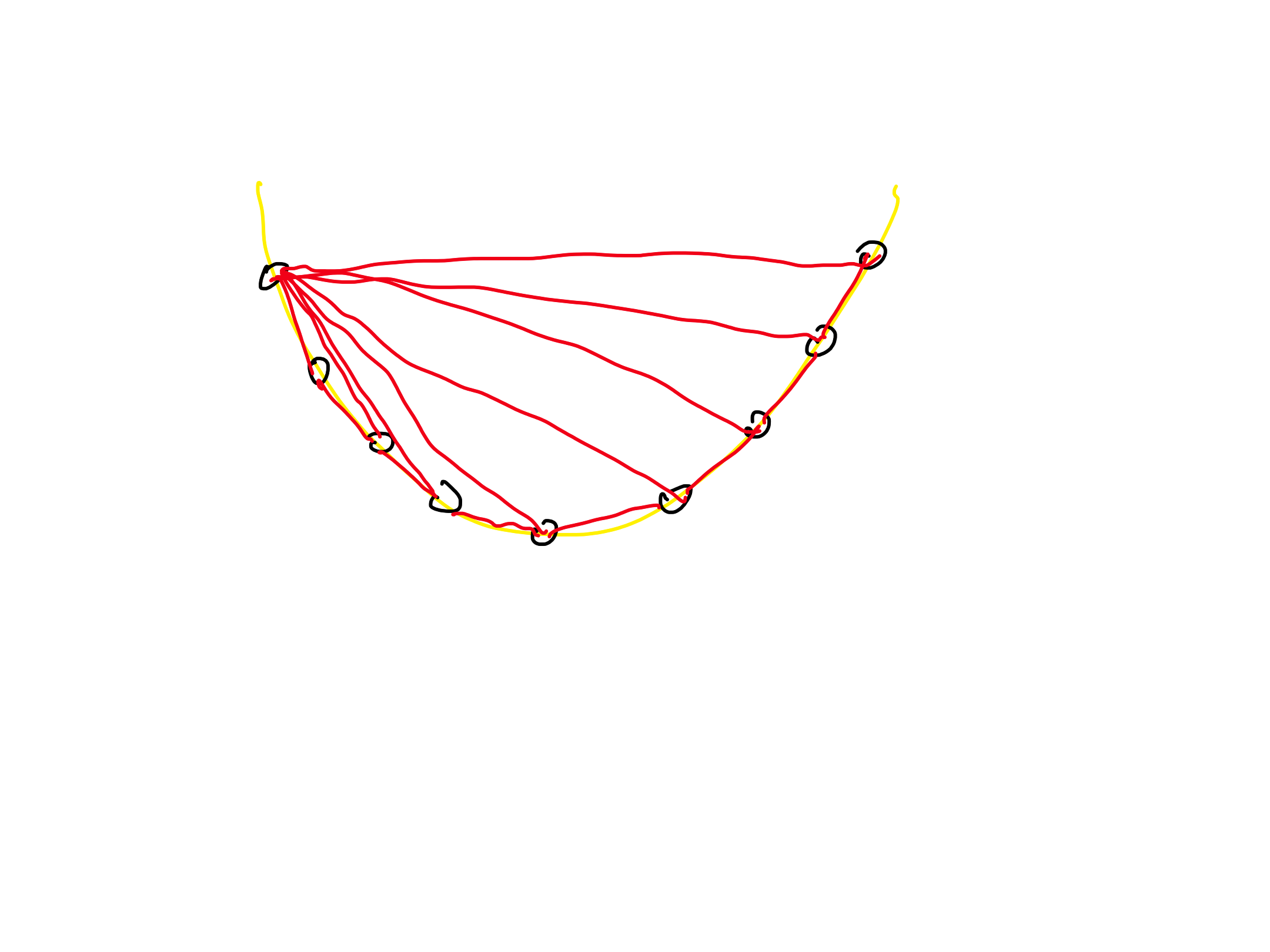
For a general $n$, describe a set $P$ of $n$ points in which at least one point occurs in $\Omega(n)$ triples when computing the convex hull of $P$ using the incremental algorithm.
Let $P$ be a set of points lying on the graph of a convex function. Then the leftmost point of $P$ will occur in $n-2$ triples when computing the upper hull. Therefore, it occurs in $\Omega(n)$ triples when using the incremental algorithm.
Exercise 3
Graham’s algorithm consists of two steps: (1) we first build a polygon $M$ from the given points, and then (2) we change $M$ until we get $\operatorname{CH}(P)$. Show that step (2) is not sufficient to compute the convex hull of a polygon: find a polygon $N$ such that immediately performing step (2) on it does not yield $\operatorname{CH}(N)$.

Exercise 4
Let $P$ be a set of points in the plane. For each point $p \in P$ we define
\[\operatorname{cell}(p)=\{ x\in \mathbb{R}^2 \mid d(x,p)\leq d(x,p') \text{ for each }p'\in P\},\]where $d(\cdot, \cdot)$ is the Euclidean distance. Show that $\operatorname{cell}(p)$ is a convex set for each point $p \in P$.
\[\operatorname{cell}(p) = \bigcap_{p' \in P} \{x \in \mathbb{R}^2 \mid d(x, p) \le d(x, p') \}\]
$\operatorname{cell}(p)$ is an intersection of convex sets and is therefore itself convex.

Exercise 5
A convex polygon $M$ is given as a list of vertices in clockwise order. Describe a linear time algorithm which sorts the vertices of the polygon $M$ by their $x$ coordinates. Can your algorithm be adapted so that it will work for any polygon $M$ (still in linear time)?

- Find the leftmost and rightmost vertex and identify the upper and lower paths
- Each path is a sorted list (by $x$), and we can merge them in linear time

For general polygons, we prove that a linear time algorithm would imply an $o(n \log n)$ time sorting algorithm.
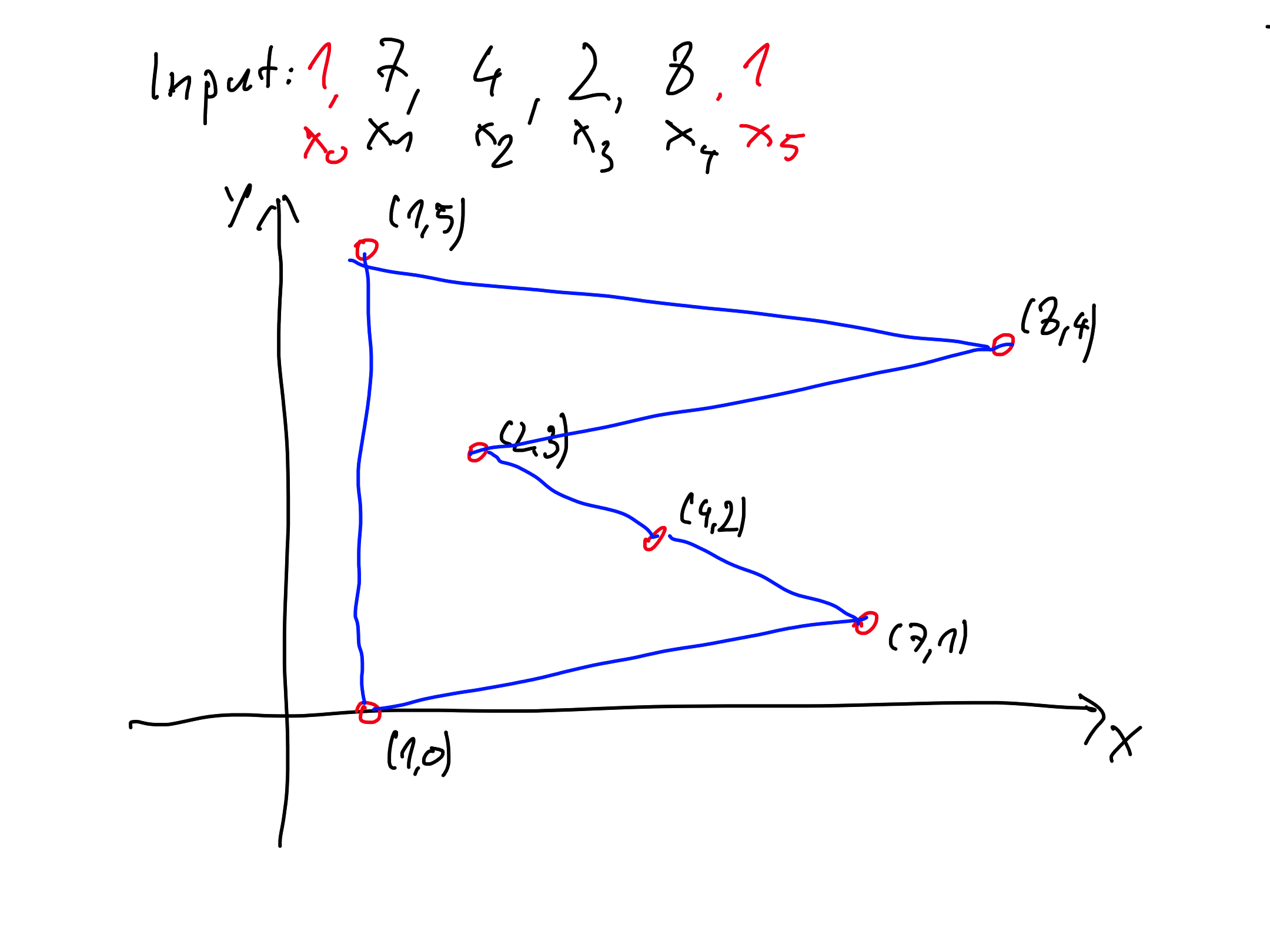
- Input: list ${x_1}, {x_2}, \dots, {x_n}$
- Objective: return a sorted list
- Set ${x_0} = {x_{n+1}} = {\min_{i=1}^n} {x_i} - 1$
- Map ${x_i} \to {p_i} = ({x_i}, i)$ ($O(n)$)
- Run our algorithm with ${p_0}, {p_1}, \dots {p_{n+1}}$ ($O(n)$)
- Return the $x$ coordinates of the output (without the first two elements) ($O(n)$)
- Time complexity: $O(n)$
Clearly, such an algorithm will take $\Omega(n \log n)$ time!