Computational Geometry
Computational geometry - Tutorial 31.3.2021
Polygons
Exercise 1
Draw the diagonals computed by the algorithm you have seen at the lectures to the $x$-monotone polygon in the figure below.

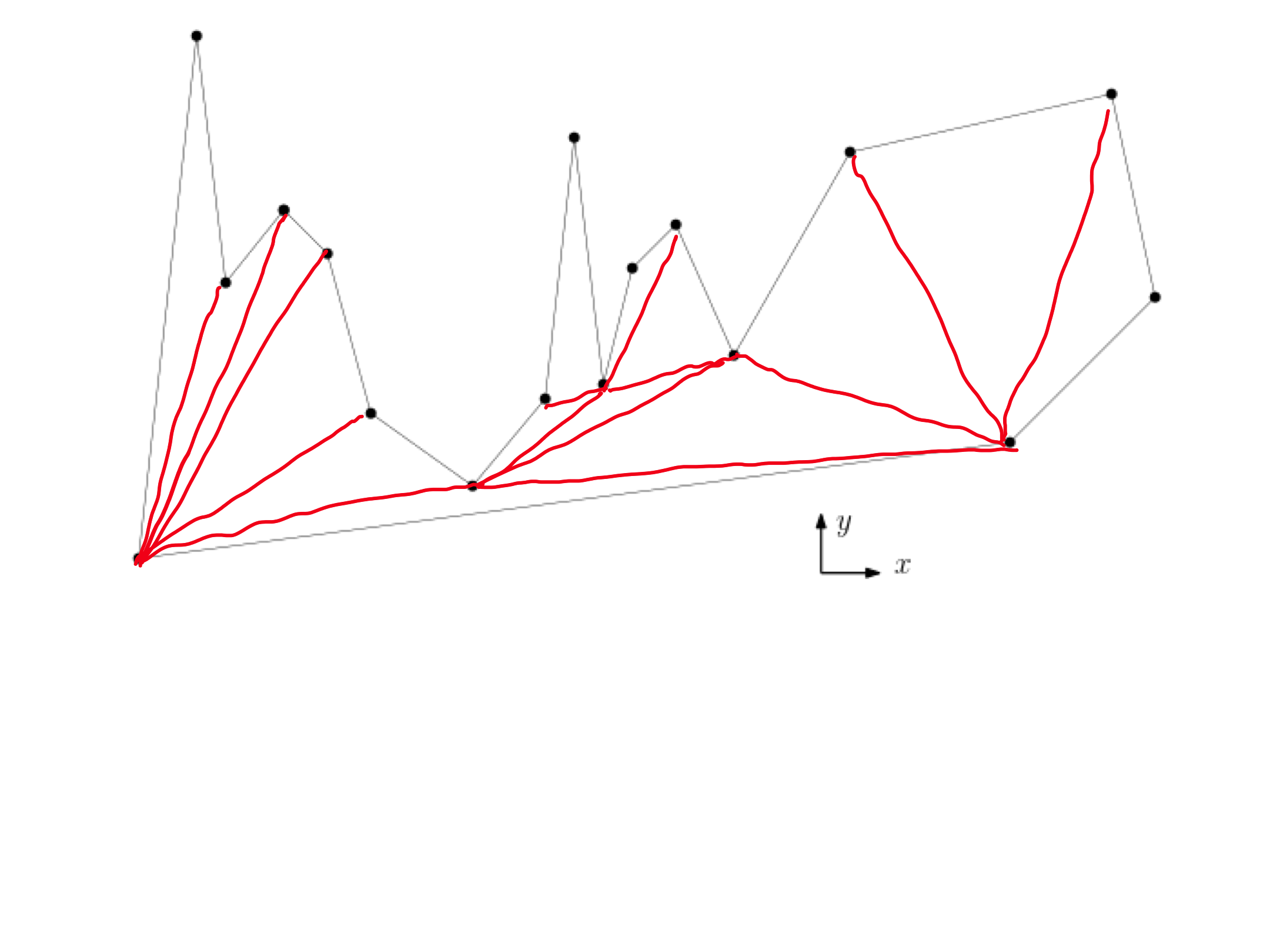
Exercise 2
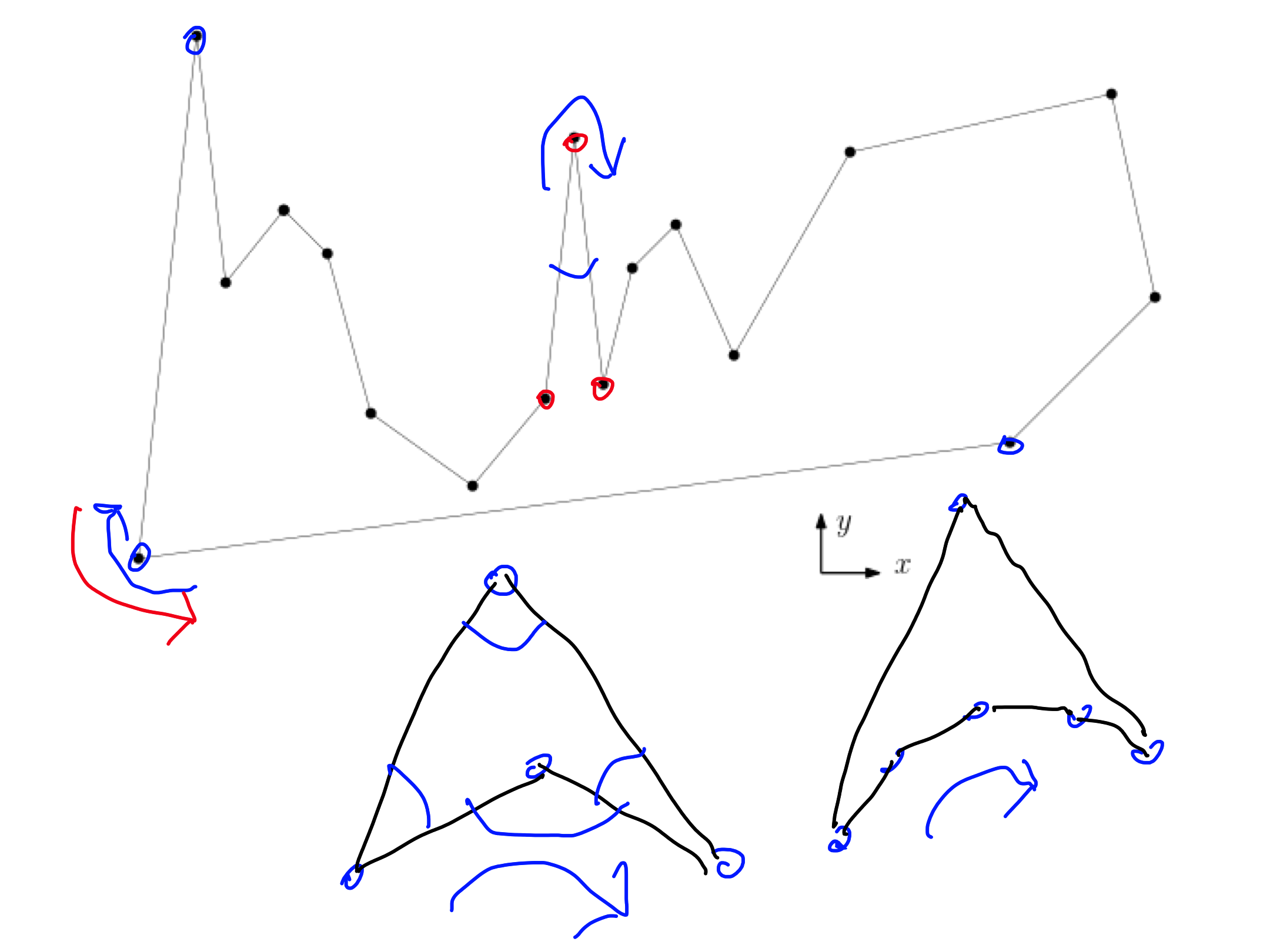
We are given a polygon as a list of vertices, but we do not know whether they are given in clockwise or counterclockwise order. Describe an algorithm which finds the order in linear time.
- Find the leftmost point ${p_1}$.
- Let ${p_0}$ and ${p_2}$ be the predecessor and successor of ${p_1}$.
- If $({p_0}, {p_1}, {p_2})$ is a right turn, then we have clockwise order, otherwise we have counterclockwise order.
Exercise 3
Describe an algorithm which, given a polygon $P$, finds a direction (if any) in which $P$ is monotone.
- For each concave vertex, determine the directions for which the vertex is a merge or split vertex.
- between the lines perpendicular to the incident edges
- Sort the endpoints of the intervals by the angle.
- Count the number of vertices for which the initial angle is “forbidden” (i.e., we have a split or merge vertex).
- Walk through the endpoints and update the count.
- If at some point the counter drops to zero, then we have a direction for which $P$ is monotone.
- Time complexity: $O(n \log n)$
A linear time algorithm for this problem exists!
Exercise 4
Write the pseudocode of an algorithm which computes a $3$-colouring of the given triangulation of a polygon in linear time.