Computational Geometry

« nazaj

Computational geometry - Tutorial 24.3.2021

---

Sweeping algorithms

Exercise 1

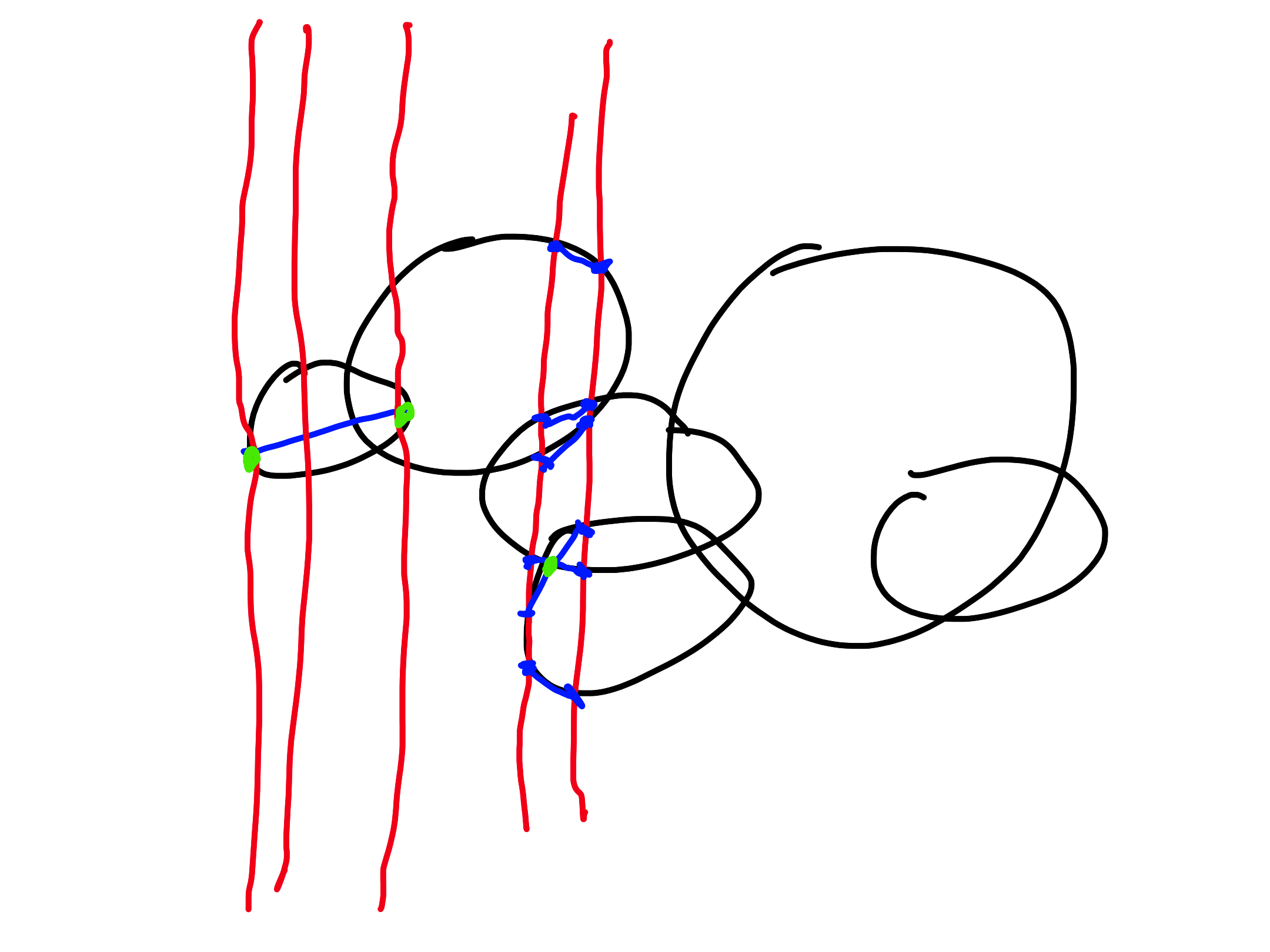
Let $S$ be a set of $n$ circles in a plane. (A circle is a curve, i.e., the edge of a disk.) Describe an output-sensitive sweeping algorithm which reports all intersections between the circles in $S$ in $O((n+k) \log n)$ time, where $k$ is the number of reported intersections.

---

• input: sequence of circles given by $(p, r)$, where $p$ is a point in the plane and $r > 0$
• output: sequence of points with pointers to intersecting circles
• event queue: binary search tree (or a modified heap)
  • leftmost points of circles
  • rightmost points of circles
  • intersections between circles
• state: binary search tree
  • upper half-circles
  • lower half-circles
• initialization:
  • event queue: add leftmost and rightmost point of each circle ($O(n \log n)$)
  • state: empty BST
• events ($O(n+k)$ steps, each taking $O(\log n)$):
  • leftmost point:
    • add upper and lower half-circles of the corresponding circle
    • check for intersections with the neighboring half-circles and add them to the queue
  • rightmost point:
    • remove upper and lower half-circles of the corresponding circle
    • check for intersections between the newly neighboring half-circles and add them to the queue
  • intersection:
    • report the intersection
    • swap the intersecting half-circles
    • check for intersections with the newly neighboring half-circles and add them to the queue

---

Exercise 2

Let $P$ and $Q$ be $x$-monotonous paths with $n$ and $m$ vertices, respectively. Assume that no $3$ vertices are collinear.

1. Prove that $P \cap Q$ has cardinality at most $O(n+m)$.
2. Describe an algorithm which computes $P \cap Q$ in linear time.

---

1. • For each pair of consecutive segments $s, s’ \in P$, there exists at most one segment from $Q$ intersecting both $s, s’$.
   • The maximal number of intersections is $n+m-3 = O(n+m)$.
   • Example list of intersections:
     • $({p_1}, {q_1})$
     • $({p_1}, {q_2})$ last
     • $({p_2}, {q_2})$ last
     • $({p_3}, {q_2})$
     • $({p_3}, {q_3})$
     • $({p_3}, {q_4})$ last
     • $({p_4}, {q_4})$

   

2. • intialization: merge the two paths into a $x$-sorted list of points ($O(n+m)$)
   • state: segments from $P$ and $Q$ the sweep line currently intersects
   • events ($O(n+m)$):
     • vertices of $P$
     • vertices of $Q$
     • action at vertex from $R \in \lbrace P, Q \rbrace$ ($O(1)$):
       • replace the segment from $R$ in the state with the next segment
       • check for the intersection with the other segment in the state

---

Exercise 3

Let $S$ be a set of $n$ pairwise disjoint segments in a plane, and let $p$ be a point not lying on any segment from $S$. Let $S(p)$ be the subset of the segments in $S$ which are partially visible from $p$ - i.e., a segment $s \in S$ is in $S(p)$ if and only if there is a point $q \in s$ such that $\overline{pq} \cap s’ = \emptyset$ for each $s’ \in S \setminus \lbrace s \rbrace$. Describe an algorithm which computes $S(p)$.

Hint: a sweeping algorithm can sweep with something which is not a line.

---

• we use a sweeping ray going around $p$
  • take polar coordinates $(r, \phi)$ with origin in $p$
• state: heap containing the segments intersecting the sweeping ray
• events: starting and ending points of segments
• output: set
• initialization:
  • event queue: sort the endpoints of segments by $\phi$ into a sorted list ($O(n \log n)$)
  • state: add the segments intersecting the sweeping ray in initial position $\phi = 0$ ($O(n \log n)$)
• events ($O(n)$):
  • starting point:
    • add the corresponding segment to the state ($O(\log n)$)
    • if the new segment is first in the state, add it to the output ($O(1)$)
  • ending point:
    • remove the corresponding segment from the state ($O(\log n)$)
    • if the segment was first in the state, add the new first segment to the output ($O(1)$)
• time complexity: $O(n \log n)$

---

Exercise 4

We are given a set $P$ of $n$ points in a plane, and two more points $q,q’ \notin P$. We are looking for the disk ${D_\min}$ which contains $q, q’$ and the least number of points from $P$.

1. Prove: if there is a disk containing $q, q’$ and $k$ more points from $P$, then there exists a disk with $q, q’$ on its boundary which contains at most $k$ points of $P$.
2. For a given point $p$, let $C(p)$ be the set of centers of the disks containing $p$ with $q, q’$ on their boundary. What is $C(p)$?
3. Describe an algorithm which finds ${D_\min}$ in $O(n \log n)$ time.

Ta stran je odprtokodna. Izboljšaj to stran.

Ta zapisek je dostopen tudi na HackMD.