Computational Geometry
Computational geometry - Tutorial 17.3.2021
Sweeping algorithms
- description of input and output
- data structure for the event queue, types of events
- data structure for the state, type of entries
- initialization of the data structures
- action at each type of event
Exercise 1
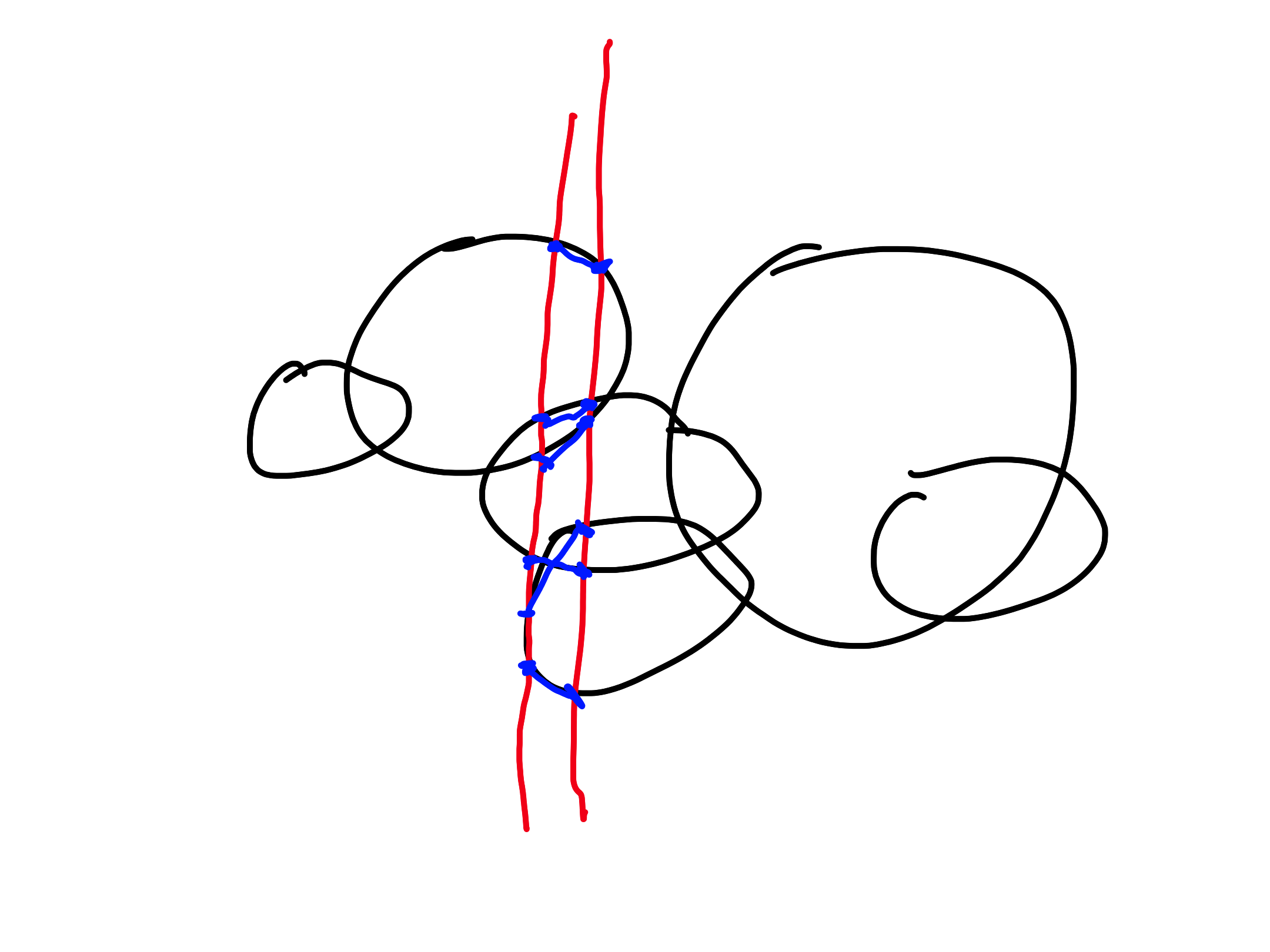
The figure below shows the segments from the set $S$. We would like to find the intersections of the segments using the algorithm we have seen on the lectures. Write down the list of pairs of segments $\lbrace s,s’ \rbrace$ ($s, s’ \in S$) for which the algorithms checks whether $s \cap s’$ is empty or not. The pairs should appear in the list in the same order as they are checked by the algorithm. If the algorithm checks a pair multiple times, then the pair should appear accordingly many times in the list.
The algorithm for finding intersection of segments as described on the lectures:
- input: sequence of segements given as $(p, q)$, where $p$ and $q$ are their endpoints (points in a plane)
- output: sequence of pairs of intersecting segments
- event queue: priority queue (dynamic BST or heap with pointers)
- leftmost points of segments (pointer to the segment, coordinates)
- rightmost points of segments (pointer to the segment, coordinates)
- intersections of two segments (pointer to the two segments, coordinates)
- state: dynamic BST
- segments
- initialization:
- add leftmost and rightmost points of each input segment to the event queue
- empty state
- events:
- leftmost point:
- add the segment to the state
- check for intersections with neighboring segments and add them to the queue
- rightmost point:
- remove the segment from the state
- check for intersection of neighboring segments and add it to the queue
- intersection:
- report the intersection
- swap the intersecting segments
- check for intersections with newly neighboring segments and add them to the queue
- leftmost point:

Exercise 2
We are given a set $S$ of $n$ pairwise disjoint segments. Each segment from $S$ has one endvertex on the line $y = 0$ and the other endvertex on the line $y = 1$. The segments of $S$ partition the strip between the lines $y = 0$ in $y = 1$. Give pseudocode for a data structure which can be constructed in $O(n \log n)$ time and can answer queries to identify the part of the strip containing the query point $p = ({p_x}, {p_y})$ ($0 < {p_y} < 1$) in $O(\log n)$ time.
- construction: sort the segments according to the $x$ coordinate of the endpoint with $y = 0$ ($O(n \log n)$)
- query: bisection according to whether the query point lies left or right of the segment ($O(\log n)$)

Exercise 3
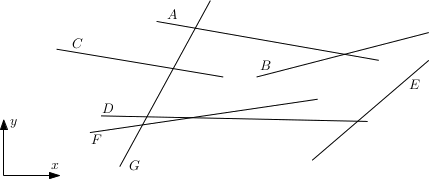
We are given a set $L$ of $n$ lines in a plane. Let $I$ be the set of intersections of the lines in $L$. Describe an algorithm that returns the smallest rectangle containing $I$ with edges parallel to the coordinate axes in $O(n \log n)$ time.

Idea: find the leftmost, rightmost, topmost and bottommost intersections
- Input: sequence of lines $ax + by = c$
- Sort lines by $(u/v, c/v)$, taking only the line with $v = 0$ which has the smallest value $c/u$ ($O(n \log n)$)
- leftmost: $(u, v) = (a, b)$
- topmost: $(u, v) = (-b, a)$
- rightmost: $(u, v) = (-a, -b)$
- bottommost: $(u, v) = (b, -a)$
- Compute intersections for neighboring pairs of lines and find the one with the smallest/largest $x$/$y$ coordinate ($O(n)$)

Exercise 4
Let $S$ be a set of $n$ circles in a plane. (A circle is a curve, i.e., the edge of a disk.) Describe an output-sensitive sweeping algorithm which reports all intersections between the circles in $S$ in $O((n+k) \log n)$ time, where $k$ is the number of reported intersections.
- input: sequence of circles given by $(p, r)$, where $p$ is a point in the plane and $r > 0$
- output: sequence of points with pointers to intersecting circles