Computational Geometry
Computational geometry - Tutorial 10.3.2021
Plane geometry
Exercise 1
Let $P$ be a set of $n$ points in a plane. Assume that no three points of $P$ are collinear. Describe an algorithm which constructs a polygon with $P$ as its vertex set in $O(n \log n)$ time.
Find an unbounded family $\mathcal{P}$ of sets of points in a plane (i.e, for any natural number $n$ there exists $P \in \mathcal{P}$ with $\vert P \vert \ge n$) with the property that for any $P \in \mathcal{P}$, there are exponentially many polygons with $P$ as their vertex set. That is, there exists a number $\epsilon > 0$ such that for each $P \in \mathcal{P}$ there exist at least $(1 + \epsilon)^{\vert P \vert}$ polygons with $P$ as their vertex set.
- sort the points according to the $x$ coordinate $O(n \log n)$
- draw a line $\ell$ through the leftmost and rightmost point $O(1)$
- construct two $x$-monotonous paths through the points above (resp. below) $\ell$ $O(n)$
Time complexity: $O(n \log n)$

Construction of ${P_n}$: $n/3$ points on each of the upper, middle and lower curves
- for each point on the middle curve, we can connect it either above or below
- therefore, there are at least $2^{n/3} = \sqrt[3]{2}^n$ polygons on ${P_n}$

Exercise 2
We are given the finite sets $R$ and $B$ of red and blue points, respectively. Assume that $R \cap B = \emptyset$ and that no three points are collinear. A matching $M \subset R \times B$ between $R$ and $B$ is a disjoint matching if the segments $\overline{rb}$ (where $(r, b) \in M$) are pairwise disjoint.
- Let $M^\ast$ be the shortest matching between $R$ and $B$ (i.e., the sum of the lengths of the segments is minimal). Prove that $M^\ast$ is a disjoint matching.
- Can we use 1. for an algorithm which finds a disjoint matching?
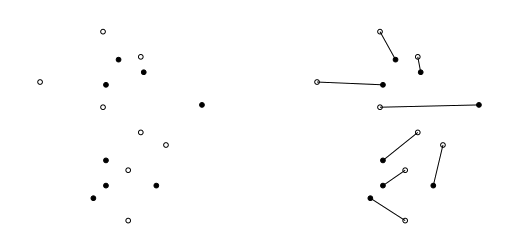
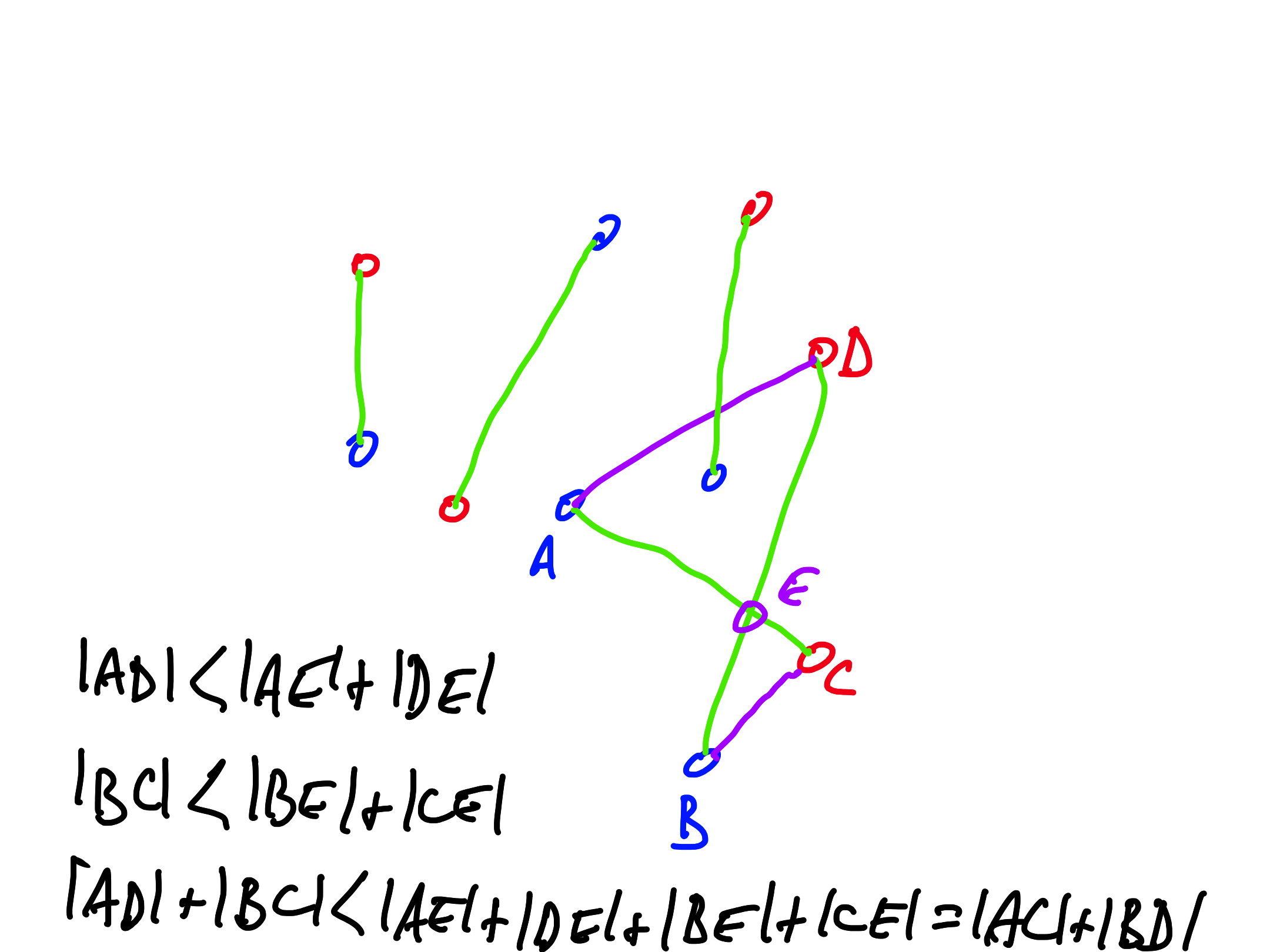
- If we have an intersection between segments $(A, C)$ and $(B, D)$, we can replace them with the segments $(A, D)$ and $(B, C)$ and obtain a shorter matching. Therefore, the shortest matcing is disjoint.
- Algorithm: while there is a pair of intersecting segments in the matching, replace them as above. Since the length of the matching decreases and there is a finite number of matchings, the algorithm eventually stops.
Exercise 3
We are given a set $P$ of $n$ points and a line $\ell$ in a plane. We are looking for the smallest disk ${D_{\min}}$ with its center on the line $\ell$ containing all points of $P$. Describe an algorithm which finds ${D_{\min}}$ in polynomial time. ($O(n \log n)$ is possible, but too hard for now.)

Algorithm:
- for each pair of points $u, v \in P$, find the circle through $u$ and $v$ centered on $\ell$ ($O(n^2)$)
- for each such circle, check that $P$ is contained in the disk bounded by the circle ($O(n^2)$ times $O(n)$)
- return the smallest such disk
Time complexity: $O(n^3)$
- to achieve $O(n \log n)$, use the sweep line paradigm
Exercise 4
Let $P$ be a set of $n$ points in a plane, and let $L$ be the set of lines passing through each pair of points of $P$. Describe an algorithm which finds the line in $L$ with the largest slope in $o(n^2)$ time.